https://huidea.tistory.com/233
[기초 통계] 통계적 가설 검정 과정 (검정통계량, P-value)
참고 link : https://blog.acronym.co.kr/621 통계적 가설 검정(Statistical Hypothesis Testing) 절차 통계적 가설 검정은 통계적 추측의 하나이다. 전체 집단의 실제 값이 얼마라는 주장에 대해서 표본을 활용해..
huidea.tistory.com
비율 검정 : 비율이 대한 통계적 유의한지 검정하는 것 - Z분포를 띈다고 가정하고 확인
- 단일 비율 검정 (one-sample proportion Ztest)
모집단 비율, 표본의 비율 두가지가 있는 경우, 해당 표본의 비율이 모집단으로부터 나온건가?
ex. A중학교에는 100명 중에 45명이 흡연을 한다. 국가 통계를 보니 중학생 흡연율은 35%라고 한다. 통계적으로 유의한가?
- 두 독립표본 비율 검정 : 독립적으로 추출된 두 독립 표본간의 비율이, 차이가 있는가?
ex. 복날에 A회사 사람들 300명 중 100명이 삼계탕을 먹었고, B회사 사람들 400명 중 170명이 삼계탕을 먹었다.
두 비율이 통계적으로 같나?
+) 두 검정 방법 모두 모집단이 정규분포라고 가정한 뒤 계산
1) 단일 표본 비율 검정 (모비율 검정, one-sample proportion test)
1.1) 가정 : 모집단은 정규분포를 띈다.
1.2) 공식

- 모비율의 신뢰구간을 추정할 대는 정규분포를 사용함
- 정규분포 공식에서 표본 평균 대신 표본 비율이 들어가고 모 평균 대신 모 비율이 들어감
- 평균의 표준편차 대신에 비율의 표준편차가 계산되어 들어감

차이 (Z값이) 큼 : 검정통계량 값 커짐 --> Pvalue 값 작아짐 --> 귀무가설 기각 "모집단 비율(phat)과 표본 비율(p0) 같지않다"
차이 (Z값이) 적음 : 검정통계량 값 작음 --> Pvalue 값 커짐 --> 귀무가설 수용 "모집단 비율(phat)과 표본 비율(p0) 같다"
ex. 코로나 지원금 차등분배
코로나 지원금 차등 분배에 대해서 대한민국 국민 찬반여부를 조사하였다.
총 1024명이 설문조사에 응답하였고, 이 중 찬성하는 비율은 82%였다.
경상권 지역 사람들만 조사하였을때 찬성하는 비율은 70% 였다.
경상권 표본 비율이 모집단 비율과 비교하여 통계적으로 유의한지 확인해보자. (신뢰구간 95% , 유의수준 0.05)

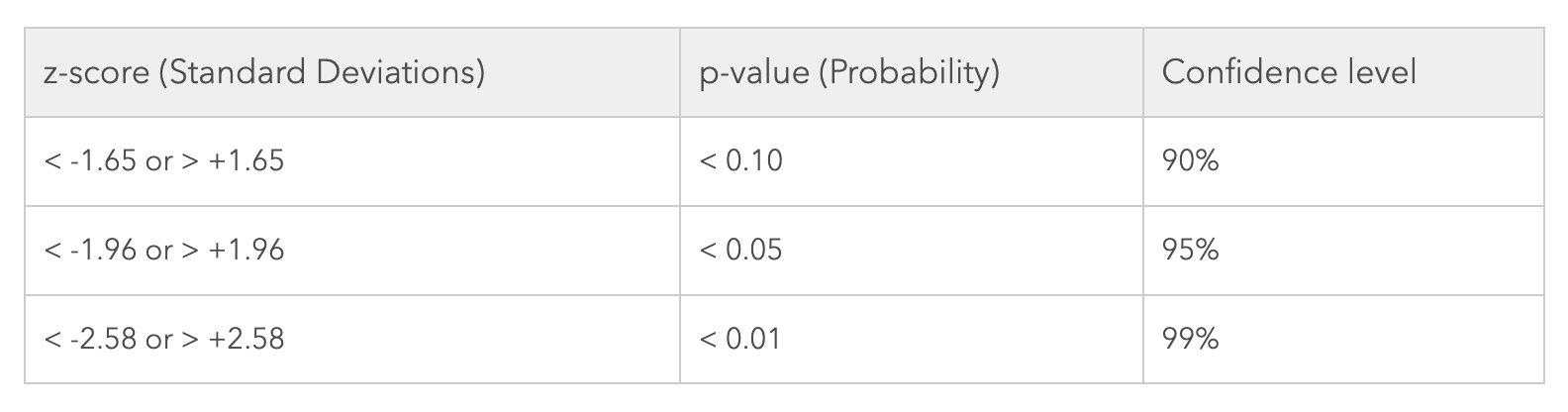
계산된 검정 통계량 (Z score) 값이 유의수준 1.96보다 훨씬 크므로 귀무가설을 기각한다.
즉, 경상권 찬성 비율과 전체 국민 찬성 비율은 통계적으로 다르다.
2) 두 독립 표본 비율 검정 (two proportion test)
: 두 모평균의 차이 μ1-μ2에 대한 신뢰구간 추정과 가설 검정 실시
2.1) 가정
- 두 모집단에서 두 표본은 무작위로 독립적으로 추출한다.
- 두 모집단은 정규 분포를 따른다.
- 두 모분산은 알려져 있다.
2.2) 예시

차이 (Z값이) 큼 : 검정통계량 값 커짐 --> Pvalue 값 작아짐 --> 귀무가설 기각 "두 집단 비율이 같지않다"
차이 (Z값이) 적음 : 검정통계량 값 작음 --> Pvalue 값 커짐 --> 귀무가설 수용 "두 집단 비율이 같다"
ex. 대학축제와 주류판매
대학축제와 주류판매를 허용해야 되는지 여부에 대해 일반인과 대학생들에게 설문조사를 실시하였다. 결과는 다음과 같았다.
| 주류판매 찬성 | 주류판매 반대 | 총 | |
| 일반인 | 362 | 409 | 771 |
| 대학생 | 249 | 483 | 732 |
일반인과 대학생들의 주류판매 허용여부에 대한 찬성비율이 같은가? (신뢰구간 95% , 유의수준 0.05)
일반인 찬성 비율 : 0.4695 (=362/771)
대학생 찬성 비율 : 0.3401 (=249/732)
phat : 0.406

Z score 5.1032 --> Pvalue 0.0000003

Z값이 1.96이상, pvalue 0.05 이하 이므로 귀무가설을 채택할 수 없음
즉, 일반인과 대학생 두 집단 비율이 같지 않다.
참고 Link :
https://rfriend.tistory.com/129
https://codlingual.tistory.com/55
'Study > Statistics & Math' 카테고리의 다른 글
| [기초 통계] 통계적 가설 검정 과정 (검정통계량, P-value) (0) | 2022.01.25 |
|---|---|
| [기초통계] t 분포, F 분포 강의 정리 (0) | 2022.01.20 |
| [기초 통계] 표본분산의 분포, 카이제곱분포 (0) | 2022.01.18 |
| [기초 통계] 표본분포(Sampling Distribution), 샘플평균의 분포 강의 내용 정리 (0) | 2022.01.18 |
| [통계] 사후설계분할표_1218 (0) | 2020.12.18 |




댓글