https://www.youtube.com/watch?v=DyBxYsCow9k&list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT&index=3
위의 강의 내용을 캡쳐 + 정리한 내용입니다.
앞의 내용 link :
https://huidea.tistory.com/228
[기초 통계] 표본분포(Sampling Distribution), 샘플평균의 분포 강의 내용 정리
https://www.youtube.com/watch?v=EjQq2s9C9Sc&list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT&index=3 고려대학교 김성범 교수님 강의를 일부 정리한 내용입니다. 1. 모집단과 표본 2. 표본 샘플링 --> 통계량 stati..
huidea.tistory.com
앞의 내용에 이어서..
0. 이전시간 핵심 키워드
통계량 : 표본의 평균과 분산
표본 분산(sampling distribution) : 통계량의 분포 즉, 표본의 평균의 분포 / 표본의 분산의 분포

* 표본 평균의 분포 --> N( 뮤,시그마제곱 / N) => 정규 분포
* 표본 분산의 분포 --> 카이제곱분포
1. 카이제곱분포 - 표준정규분포 제곱의 합
1) 정의

1) 확률 변수 Z1 ~ Zn 각각이 표준 정규 분포를 따르게 됨 N(0,1)
2) 표준 정규분포 각각 제곱을 한뒤 더하면 ?

3) Z는 카이제곱 분포를 따르게 되는 것임

** 여기서 v 는 자유도 (파라미터) 인데, 표준 정규 분포를 각각 몇 개 더해줬는지를 뜻함
2) 카이 제곱 그래프 - skew to the right (자유도 4)

3) 카이 제곱 분포 - 확률 (정규분포처럼 특정값 보다 클 확률 표로 계산함)

Y 값이 X**2av보다 클 확률 => 알파

알파와 자유도가 주어짐
if alpha 0.95 & v(자유도) 5 ==> X**2av = 1.145
위의 그림 처럼 다시 유도하면, P( Y >= 1.145) = 0.95 (Y 값이 1.145보다 클 확률은 0.95)
2. 표본 분산 ( 그중에서도 표본의 분산의 분산) 이 카이제곱 분포를 따른다 !! **
1) 표본 분산
+) (분산은 편차 제곱의 합 / 관측치개수) 근데 n-1인건 모집단의 분산이 아니라 표본집단의 분산이기 때문

* 여기서 n의 샘플의 개수
(분산은 편차 제곱의 합 / 관측치개수)
* Xi는 각각 독립된 정규분포
+) 자유도는 ?????
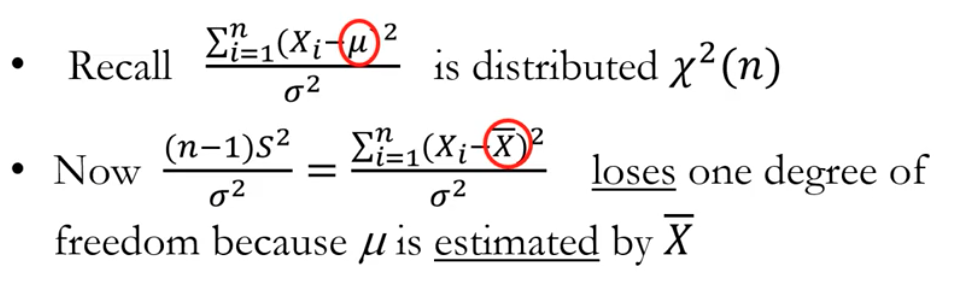
(Xi - 뮤)제곱의 합 / 분산 ==> 표준정규분포 의 제곱 !! ==> 카이제곱 분포
뮤는 모집단의 평균이자 샘플의 평균 Xbar의 값은 알고 있음
--> 따라서 n개중 1개는 알고 있으므로 모르는 건 n-1
--> 자유스럽게 값을 가질 수 있다~~~~
--> 자유도 n-1 입니다.!
더 자세히 보자면,
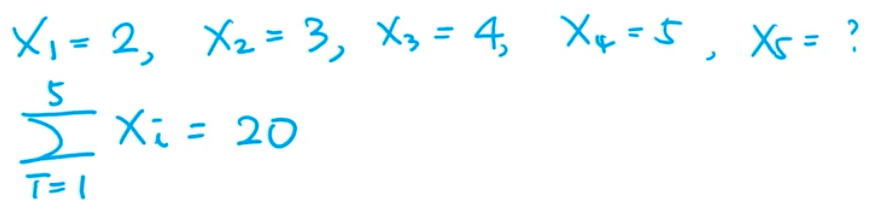
이렇게 되었을 때 X5는 6
이런 문제에서 자유도는 ? 4
--> sum이 주어지기때문에 나머지 하나는 고정값, 4개는 자유롭게 정할 수 있음 ~!
2) 표본 분산 예제
 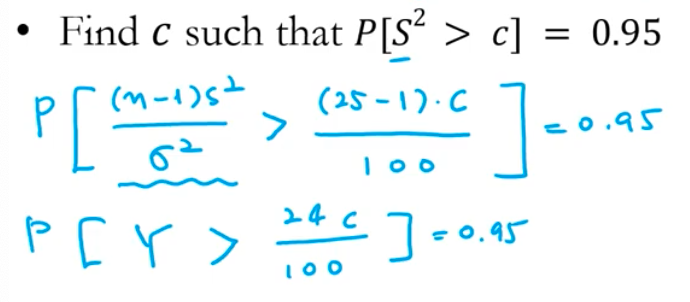 |
문제 : 모집단 (평균 15, 분산 100) 모집단에서 샘플링 개수 25개 Y (표본의 분포)는 자유도 24의 카이 분포 형태임 -> 자유도 24개 (1개는 정해지게 됨) 표본분산이 C 값보다 클 확률이 0.95 --> C값을 구하라 |
S제곱을 바로 구할 수는 없음 카이제곱 분포를 따르는 건
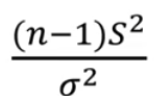
이기 때문에 이렇게 바꿔줘야함
--> n-1곱하고 모집단분산(뮤제곱)으로 나누고
==> 카이제곱 분포표를 통해 구한 값 13.848
*** 24*C/100 = 13.848 => C = 57.7

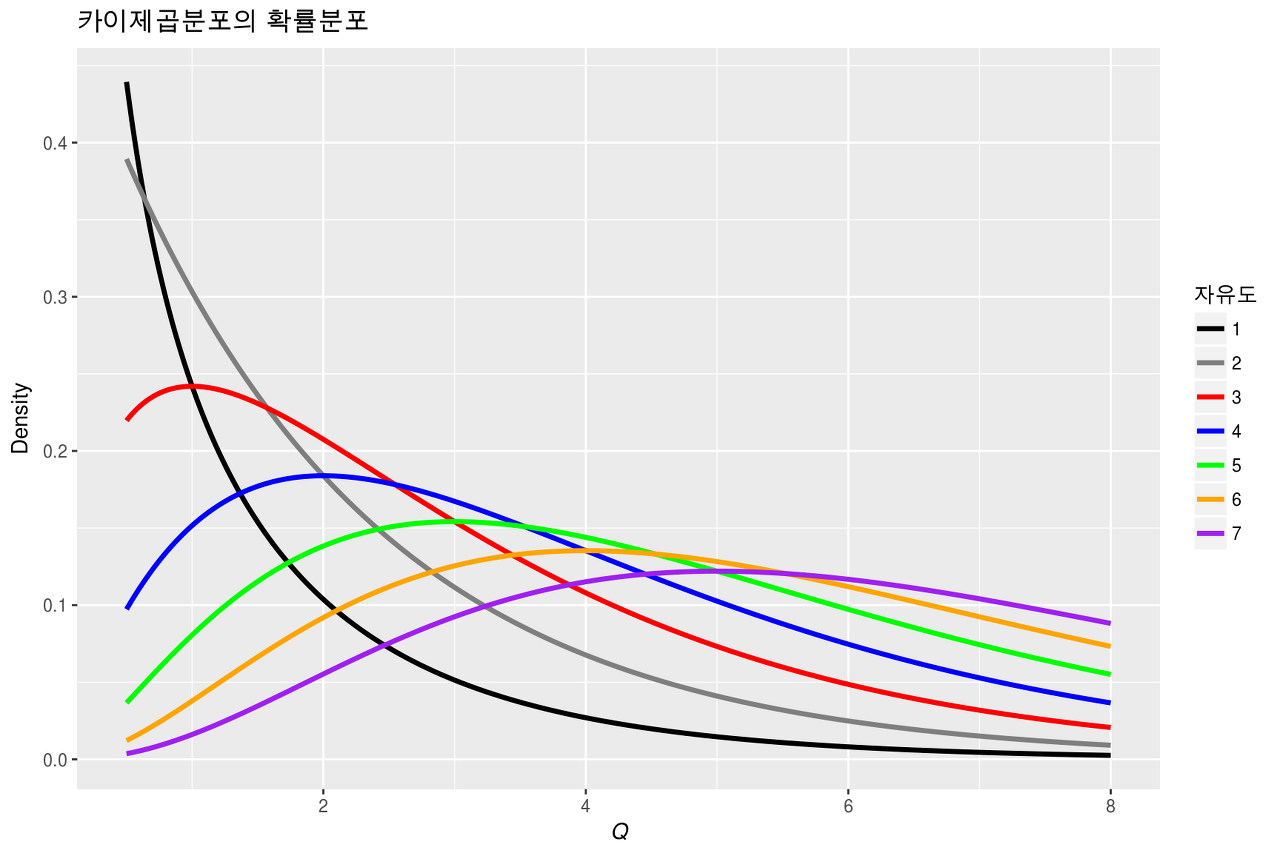
+) 자유도에 따른 그래프의 변화
'Study > Statistics & Math' 카테고리의 다른 글
| [통계] 단일 표본 비율검정 (one-sample proportion test), 독립 표본 비율 검정 (two-sample proportion test) (0) | 2022.05.09 |
|---|---|
| [기초 통계] 통계적 가설 검정 과정 (검정통계량, P-value) (0) | 2022.01.25 |
| [기초통계] t 분포, F 분포 강의 정리 (0) | 2022.01.20 |
| [기초 통계] 표본분포(Sampling Distribution), 샘플평균의 분포 강의 내용 정리 (0) | 2022.01.18 |
| [통계] 사후설계분할표_1218 (0) | 2020.12.18 |




댓글