https://www.youtube.com/watch?v=EjQq2s9C9Sc&list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT&index=3
고려대학교 김성범 교수님 강의를 일부 정리한 내용입니다.
1. 모집단과 표본

2. 표본 샘플링 --> 통계량
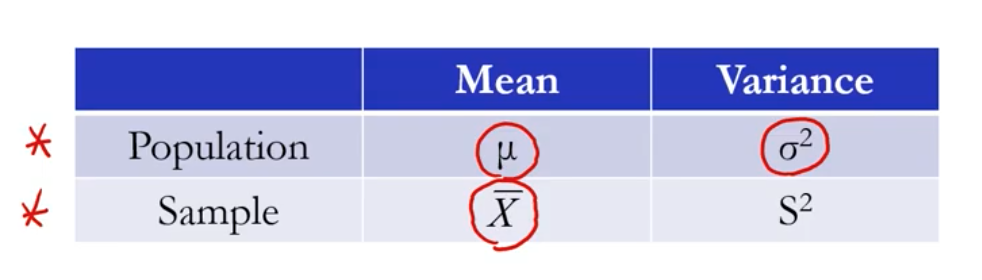

statistic : 단일 통계량을 의미
statistic : 여러개의 통계량 --> 샘플링 데이터의 함수 !
통계학의 3가지 함수
1) 확률 변수 - Random Variable : 실험으로 나온 표본들을 실수로 바꿔주는 것
ex. 동전 앞 뒤면 --> 0,1
2) 확률 함수 - 확률 변수에서 나온 실수를 0~1 사이의 확률로 바꿔주는 함수
ex. 동전 앞 뒤면 --> 0.5, 0.5
3) 통계량
샘플의 평균은 통계량, 샘플의 분포는 통계량 --> 즉 샘플 데이터로 구성된 함수면 통계량임 !
3. 표본 분포 sampling distribution
[ X bar ]
표본 분포 : 통계량의 분포****
즉 샘플의 평균의 분포 / 샘플의 분포의 분포

| # 샘플의 평균(X bar) 의 분산 : 뮤 (모집단의 평균과 같음) | # 샘플의 평균(X bar)의 분산 : 시그마 제곱/n (모집단 분산/n) |
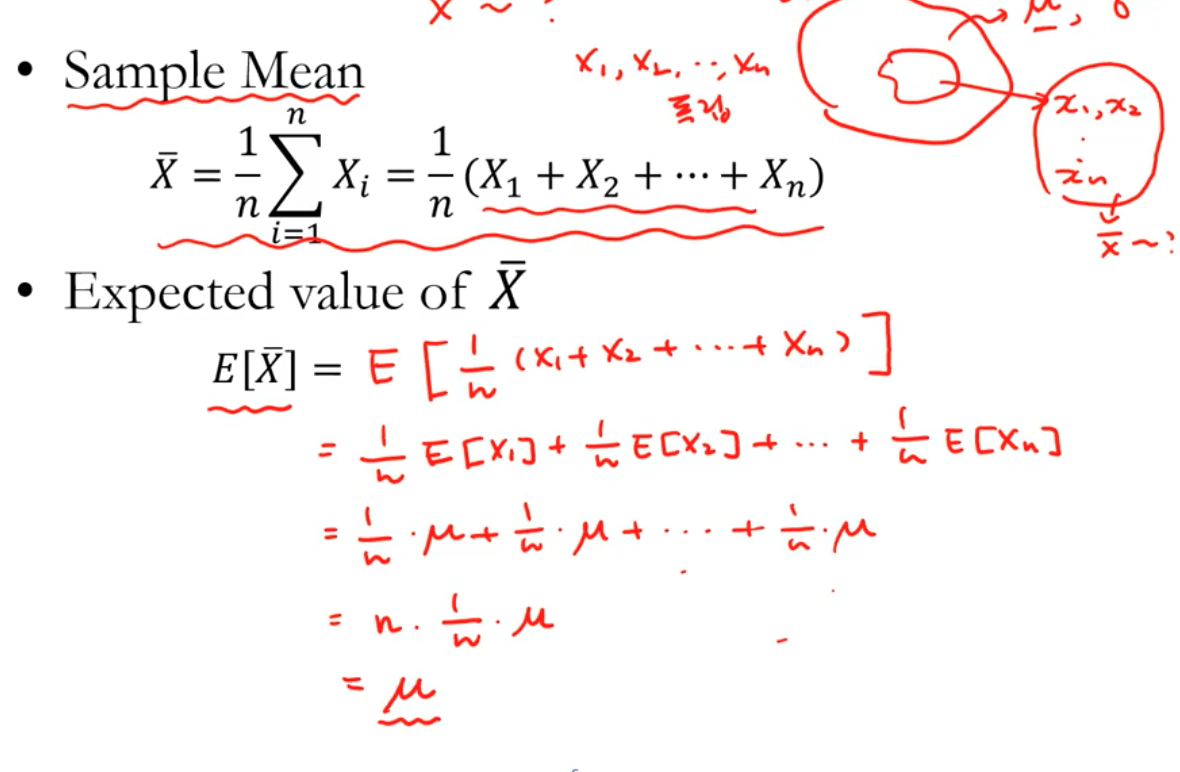 |
분산 : 편차 제곱의 평균 // 상수항은 제곱되어서 나옴 (따라서 1/n**2)  |
정리하자면 !

==> 만약 모집단의 분포가 정규분포면 N(뮤, 시그마제곱)

--> X1 ~ Xn 동일한 분포에서 iid로 뽑혔다면
--> 샘플 평균(Xbar) 의 분포는 --> N(뮤, 시그마제곱/n) 이게 바로 Sampling distribution
--> 표준 정규 분포 Z 변환하면, N(0,1)
Q. 예제

X1~X25까지 iid의 샘플 --> 모집단의 평균은 15, 분산은 100
샘플링의 평균이 20이하일 확률은 ? --> 표준 정규분포로 변환 --> 표준정규분포표로 확률 구하기
4. 중심극한정리 (만약 모집단이 정규분포가 아니라면? 표본은?)
==> 3에서는
모집단이 정규 분포를 따르면, 표본도 정규 분포
==> 중심극한정리에서는
표본의 개수(N)가 클 경우 모집단의 분포가 정규분포건 아니건 상관없이 표본들의 평균을 구하면 정규 분포다.
(모집단이 포아송 분포건 무슨 분포건 간에)
n은 샘플링 데이터 갯수 (샘플링 그룹 개수는 아님)



5. 모집단이 2개인 경우
# 두 모집단 평균의 차이를 구하고 싶다면? 뮤1- 뮤2

# 만약 두 모집단 모두 정규분포라면 ? 두 모집단 각각의 표본 평균의 차이도 정규분포
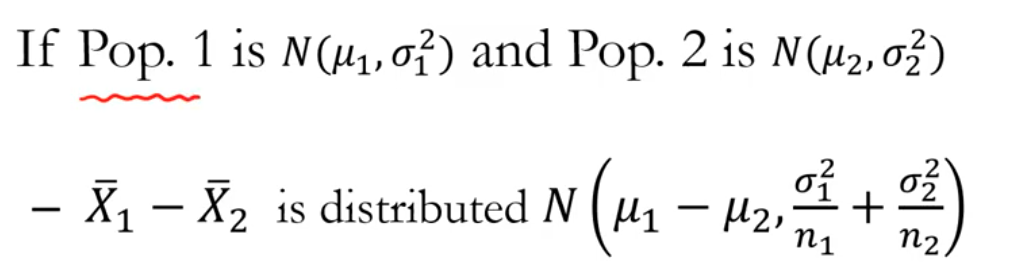
6. 표본 분포 sampling distribution - 샘플 분산에 대한 분포 (S**2 분포)

--> 샘플 분산의 분포는 계산으로 쉽게 안구해짐...
그러나 n-1 을 곱하고 모집단 분산(시그마제곱) 으로 나눴누면 구해짐, => 카이 제곱 분포
n-1, 시그마제곱은 상수이기에 분포에 변동을 안미침
따라서 표본 분포 중 샘플 분산에 대한 분포는 --> 카이제곱 분포를 따른다 ! 라고 말해도 됨
'Study > Statistics & Math' 카테고리의 다른 글
| [통계] 단일 표본 비율검정 (one-sample proportion test), 독립 표본 비율 검정 (two-sample proportion test) (0) | 2022.05.09 |
|---|---|
| [기초 통계] 통계적 가설 검정 과정 (검정통계량, P-value) (0) | 2022.01.25 |
| [기초통계] t 분포, F 분포 강의 정리 (0) | 2022.01.20 |
| [기초 통계] 표본분산의 분포, 카이제곱분포 (0) | 2022.01.18 |
| [통계] 사후설계분할표_1218 (0) | 2020.12.18 |




댓글