https://www.youtube.com/watch?v=DyBxYsCow9k&list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT&index=4
김성범 교수님 머신러닝 강의의 20분 이후 내용입니다.
강의 앞부분 내용은 :
https://huidea.tistory.com/230
[기초 통계] 표본분산의 분포, 카이제곱분포
https://www.youtube.com/watch?v=DyBxYsCow9k&list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT&index=3 위의 강의 내용을 캡쳐 + 정리한 내용입니다. https://huidea.tistory.com/228 통계량 stati.." data-og-host="hu..
huidea.tistory.com
3. T분포
1) 공식
Z 확률 변수 : N(0,1) 표준정규분포를 따른다.
Y 확률 변수 : 카이제곱 분포 (자유도가 v인)
T 통계 분포는 -->
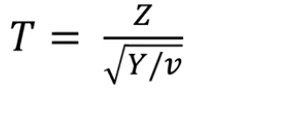
표준정규분포(Z)가 분자, 카이제곱 분포(Y)를 자유도(v)로 나눈 값이 분모 --> 이게 T분포의 정의
- T분포에서도 자유도(v) 가 파라미터 ==> t(v) 로 표기
- T분포의 평균 E(T)는 0 이고, 대칭인 형태
- 하지만 정규 분포에 비해서는 꼬리가 긴 모습 --> 비정규 분포로 분류가 됨 !!!
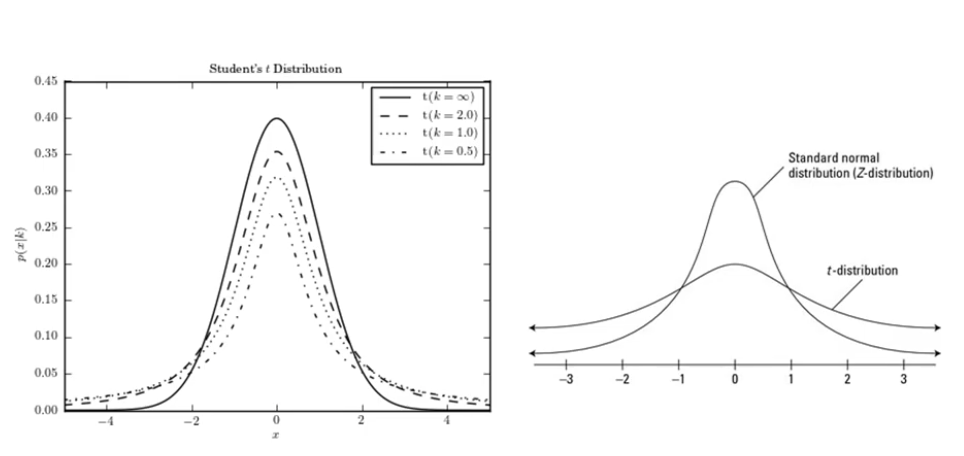
- 마찬가지로 T분포에서 특정 알파값이 어디에 속할지 확률을 계산할 때 테이블로 해석을 함
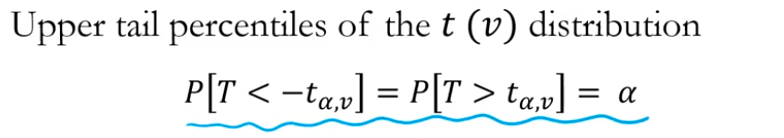
2) 유도 과정
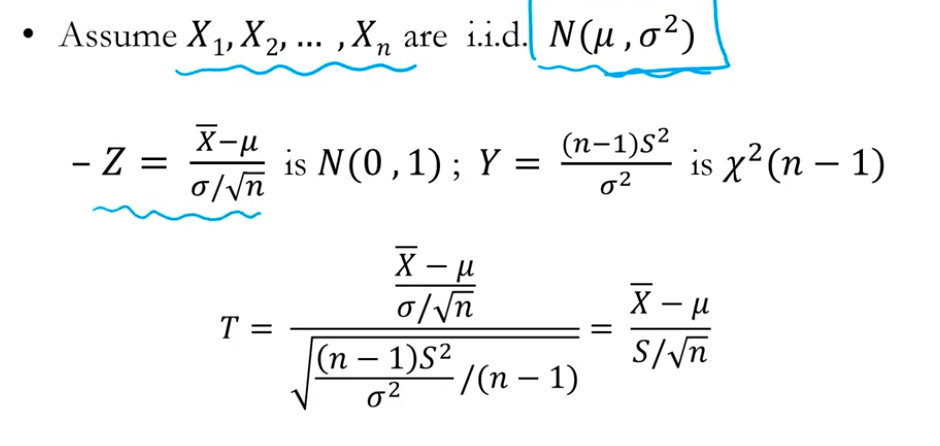
* 모집단이 여전히 정규분포 --> 여기서 X1, ~~ X25 샘플 추출
* Z는 정규분포, Y는 카이제곱분포
* T도 정규분포 형태랑 비슷하게 나옴 대신 시그마(모집단 표준편차) 대신 S(표본의 표준편차)
--> 따라서 모집단의 표준편차를 모를때, T분포를 사용함 ((응용통계에서 자주 사용하는 방법))
==> T ~ t(n-1) 로 표기 !
3) 풀이
모집단의 평균이 15, 분산이 100 인 정규분포를 따를때, 그로부터 독립적으로 동일하게 25개 추출

--> 자유도가 24인 T분포에서 C 보다 작은 값이 등장할 확률 0.05다 C값 찾아라
v = 24, 알파 0.05 => C = - 1.711 (C값보다 작은 값들 등장확률이니까)
4. F분포 : 두 카이제곱 분포의 비율
1) 공식
두 개의 카이제곱 분포를 따르는 확률 변수
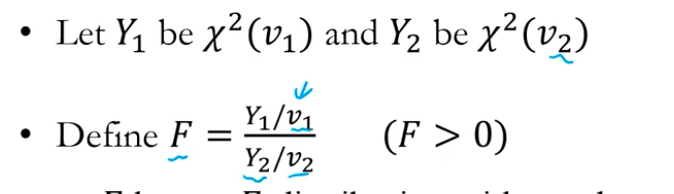
파라미터는 2개 v1, v2 --> F(v1,v2)
2) 확률 계산 방법
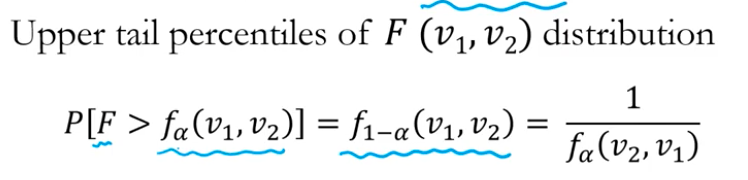


* 두개의 모집단에서 각각 샘플 추출
1) n1 개 샘플 추출 -- 추출된 표본의 분산 S1
2) n2 개 샘플 추출 -- 추출된 표본의 분산 S2
* 카이제곱분포 / 자유도1 // 카이제곱분포 / 자유도2 -
* F 분포의 파라미터는 자유도1,2 ==> F(n1-1, n2-1)

3) 예제

* 모집단1 평균 4, 분산 16 --> 15개 뽑아 // 모집단2 평균 12, 분산 48 --> 10개 뽑아
* 두 샘플의 F분포는 평균 14, 분산 9
* 이 F분포에서 표본분산비율이 c값보다 적을 확률이 0.05 --> 여기서 c를 찾아라
표본분산비율 == 1 (두 분산이 같다) // 분자, 분모의 대소를 통해 파악

+))

* 양변에 시그마제곱 분수를 곱해줘서
F 분포 테이플로 볼 수 있게 만듦
+)) 그리고 마지막에 -.95는 데이블에서 찾기 힘듦 --> 앞에서 나온 공식대로 역수를 취해서 테이블 해석 !!

'Study > Statistics & Math' 카테고리의 다른 글
| [통계] 단일 표본 비율검정 (one-sample proportion test), 독립 표본 비율 검정 (two-sample proportion test) (0) | 2022.05.09 |
|---|---|
| [기초 통계] 통계적 가설 검정 과정 (검정통계량, P-value) (0) | 2022.01.25 |
| [기초 통계] 표본분산의 분포, 카이제곱분포 (0) | 2022.01.18 |
| [기초 통계] 표본분포(Sampling Distribution), 샘플평균의 분포 강의 내용 정리 (0) | 2022.01.18 |
| [통계] 사후설계분할표_1218 (0) | 2020.12.18 |




댓글