Q. Markov Chain을 고등학생에게 설명한다면 어떤 방식이 좋을까요?
Q. Markov Chain 은 머신러닝 알고리즘 중 어디에 활용이 되나요?
Q. 깁스 샘플링 은 무엇인가
Q. 깁스 샘플링 은 왜 쓰는가 ?
Q. Markov Chain을 고등학생에게 설명한다면 어떤 방식이 좋을까요?
sites.google.com/site/machlearnwiki/RBM/markov-chain (제가 보려고 여기에 다시 옮겨 적어유 원문은 링크로 ! )
Markov Chain - MLWiki
마코프 체인 마코프 체인(Markov Chain)은 마코프 성질(Markov Property)을 지닌 이산 확률 과정(Discrete-time Stochastic Process)을 의미한다 마코프 성질 마코프 성질이라 함은 n+1회의 상태(state)는 오직 n회에��
sites.google.com
마코프 체인은 마코프 성질을 지닌 이산 확률 과정이라고 합니다.
** 여기서 이산 확률이란 ? 셀 수 있는 떨어져있는 확률 변수 즉, 이산형 데이터 (ex. 주사위 1,2,3,4,5,6 떨어져있음 연속형 수치 아님)의 확률
마코프 성질 : 예를 들어 5번째의 상태가 4번째의 상태 혹은 그전 2단계의 상태에만 영향을 받는 것
n+1회의 상태(state)는 오직 n회에서의 상태, 혹은 그 이전 일정 기간의 상태에만 영향을 받는 것을 의미
예를 들면 동전 던지기는 독립 시행이기 때문에 n번째의 상태가 앞이던지 뒤이던지 간에n+1번째 상태에 영향을 주지 않음
하지만 1차 마르코프 체인은 n번째 상태가 n+1번째 상태를 결정하는데 영향을 미친다.
(시간 t에서의 관측은 단지 단지 최근 r개의 관측에만 의존한다는 가정을 하고 그 가정하에서 성립)
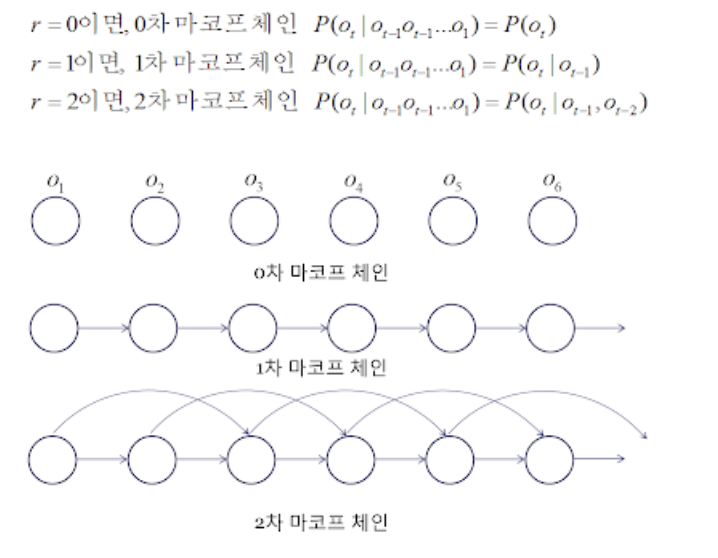
마코프 연쇄 (마코프 체인) :
마코프 연쇄(Markov Chain)란 마코프 가정(Markov assumption)을 따르는 이산 시간 확률 과정
마코프 가정은 러시아 수학자 마코프가 1913년경에 러시아어 문헌에 나오는 글자들의 순서에 관한 모델을 구축하기 위해 제안된 개념
특정 시점의 상태 확률은 단지 그 이전 상태에만 의존한다는 것이 핵심
즉 한 상태에서 다른 상태로의 전이(transition)는 그동안 상태 전이에 대한 긴 이력(history)을 필요로 하지 않고
바로 직전 상태에서의 전이로 추정할 수 있음

 |
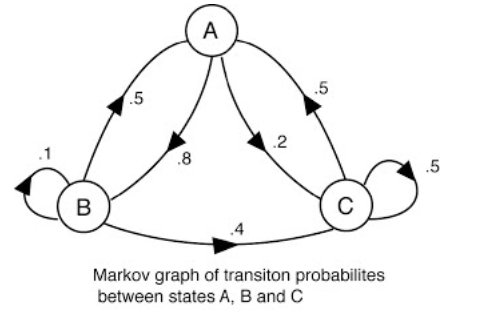 |
각 숫자가 A 상태에서 B상태로 바뀔때의 상태 전이확률을 나타내는 것 !
예제 : 1차 마코프 가정을 이용하여 확률을 계산해보자.
|
오늘의 날씨 |
내일의 날씨 |
||
|
맑음 |
비 |
흐림 |
|
|
맑음 |
0.8 |
0.05 |
0.15 |
|
비 |
0.2 |
0.6 |
0.2 |
|
흐림 |
0.2 |
0.3 |
0.5 |
날씨 상태 천이 확률표
날씨 영역은 세 가지 상태(S={맑음, 비, 흐림})를 나타낸다. 그리고 날씨는 천이 확률표와 같이 확률값 P(qn | qn-1)에 따라 다른 상태로의 천이가 이루어진다. 오늘 날씨(q1)가 "맑음"일 경우에 내일 날씨(q2)가 "맑음"이 되고 모레 날씨(q3)가 "비"가 될 확률은 얼마일까?
P(q2=맑음, q3=비 | q1=맑음)
= P(q3=비 | q2=맑음, q1=맑음) ·P(q2=맑음|q1=맑음)
= P(q3=비 | q2=맑음)·P(q2=맑음|q1=맑음) <- 마코프 가정
= 0.05 x 0.8
= 0.04
위 계산 과정에서 1차 마코프 가정에 의해 P(q3=비 | q2=맑음, q1=맑음) = P(q3=비 | q2=맑음) 가 된다. 그렇다면 어제, 오늘의 날씨가 각각 q1=비, q2=흐림 일 때, 내일 날씨가 q3= 맑음 이 될 확률은 얼마일까?
P(q3=맑음 | q2=흐림, q1=비)
= P(q3=맑음 | q2=흐림) <- 마코프 가정
= 0.2
고등학생이 이해할 수 있도록 더 쉽게 정리하자면...(요즘고등학생들 똑똑하던뎅(
일반적으로 주사위 2개를 던지는게 이산 확률 분포라면 ( 결과 2~12 각각의 독립적인 확률 계산할 수 있음 )
모두의 마블에서 주사위를 2개 던진 뒤 이동한 칸 수가 마코프 체인과 비슷한 개념이다.
바로 직전에서 이번에 어디로 이동하는지에 따라 주사위 나온 숫자 *2 배만큼 이동할 수도 있고 벌칙이 있을수도 있어서 (상태전이확률)
컨셉은 " 어디에서 부터 왔냐가 현재 상황에 영향 " 을 미친다는 것이다.
" 출신이... 영향을 미친다 ..! "
Q. Markov Chain 은 머신러닝 알고리즘 중 어디에 활용이 되나요?
==> MCMC마코프체인 몬테카를로 샘플링 기법, (그리고 이것은 깁스샘플링의 시작점)
+) 뒤에 붙은 몬테 카를로는 뭔가?
기본 컨셉 - 무작위로 난수를 생성한다 / 생성된 난수를 기반으로 구하고자 하는 정보 확률 계산 /
실험 횟수가 많아 질수록 난수 생성이 우리가 원하는 정보의 실제값과 근사해짐
" 쨋든 여러번 뽑고 이 확률을 기반으로 하는 계산법 정답 같은 놈이 나온다" 이 말이다.
이게 샘플링에서는 랜덤으로 표본을 뽑아 함수의 값을 확률적으로 계산하게 되는 알고리즘을 말한다.
정리하자면 MCMC 는 Markov Chain 을 이용한 Monte Carlo 방법.
# MCMC는 쉽게 설명해서 이전의 샘플이 다음 샘플의 추출에 영향을 준다.
즉 i번 추출의 표본을 토대로 i+1번째 표본을 뽑는 것. 마코프 체인기본 컨셉과 유사하다.
이건 특정 알고리즘이라기 보다는 Markov Chain과 Monte Carlo라는 두가지 수학적 특성을 기반으로 이루어진
샘플링 개념이라 이해하면 좋을 것 같다.
우선 마코프 체인은 연쇄를 반복하다보면 현재 상태의 확률이 직전 상태의 확률과 수렴하게 되고,
이 평형상태에 도달한 확률 분포를 정적분포(Stationary Distribution) 라고 함
이 정적 분포가 목표 분포 target distribution
그리고 이 개념으로 적용하는데 이게 마코프체인 몬테카를로 샘플링 기법 !
www.secmem.org/blog/2019/01/11/mcmc/
Markov Chain Monte Carlo 샘플링의 마법
이번 포스트에서는 강력한 샘플링 기법 중 하나인 Markov Chain Monte Carlo(MCMC)에 대해 알아보겠습니다. MCMC의 활용도는 굉장히 넓어서 머신러닝을 비롯한 베이지안 통계학, 통계물리학, 컴퓨터비전,
www.secmem.org
Q. 깁스 샘플링은 무엇인가?
ratsgo.github.io/statistics/2017/05/31/gibbs/
Gibbs Sampling · ratsgo's blog
이번 글에서는 깁스 샘플링(Gibbs Sampling)에 대해 간단히 살펴보도록 하겠습니다. 이번 글 역시 고려대 강필성 교수님 강의와 위키피디아, ‘밑바닥부터 시작하는 데이터과학(조엘 그루스 지음, ��
ratsgo.github.io
깁스 샘플링을 명확히 이해하기 위해선 몬테카를로 / 마코프 연쇄 / MCMC 각각의 연관성을 이해하면 좋은데
- 몬테 카를로 : 모든 샘플이 독립이고 생성될 확률 또한 랜덤
- 마코프, MCMC : 다음번 생성될 샘플은 현재 샘플의 영향을 받음
- 깁스 샘플링 : 다음 번 생성 표본은 현재 샘플에 영향을 받지만, 나머지 변수는 그대로 두고 한 변수에만 변화를 줌 !
( 몬테 타를로와 MCMC 사이 그 어디쯤에 있는 것이... 깁스 샘플링 같음.... )
설명 예시 (출처 : ratsgo.github.io/statistics/2017/05/31/gibbs/)

Q. 깁스 샘플링을 왜 사용하나요?
위의 예시를 살펴보면, 깁스 샘플링은 표본 전체 X0 를 고려해서 그 다음 X1 을 뽑는게 아니라,
X0 중에서도 각각의 변수 ( x01, x02, x03 )의 일부는 고정하면서 조건부 분포로 다음 X1 의 요소 (x11, x12, x13)을 추출하는 개념이다.
따라서 마코프 연쇄 과정에서 전체 표본이 아니라 아닌 각각의 변수로 샘플링을 하기 때문에
고차원의 문제를 1차원의 문제로 바꾸어 쉽게 샘플링을 할 수 있게 된다.
즉, 차원이 너무 큰 경우 깁스 샘플링을 사용해야함 !!!
Gibbs Sampler (깁스 샘플링)
Gibbs Sampler (Geman and Geman, 1984)는 MCMC Alogrithm의 특별한 방법 중 하나이다. 즉, Gi...
blog.naver.com
이 개념은 또, 토픽 모델링이랑 이어진다는 데 그것은 내일 해보기로 !
'Study > Machine learning' 카테고리의 다른 글
| [Machine learning] 나이브베이즈확률, 나이브베이즈모델 (day4 / 201013) (0) | 2020.10.14 |
|---|---|
| [Machine learning] 잠재디리클레할당 (day3 / 201012) (0) | 2020.10.12 |
| [Machine learning] 차원축소, PCA, SVD, LSA, LDA, MF 간단정리 (day1 / 201009) (0) | 2020.10.10 |
| [Machine learning] PCA(주성분분석), LDA(선형판별분석법), SVD (행렬분해) (쉽게 설명하는 차원 축소 기법들 총정리 part2) (0) | 2020.08.06 |
| [Machine learning] PCA 주성분분석 (쉽게 설명하는 차원 축소 기법들 총정리 part1) 200803 (3) | 2020.08.03 |




댓글