Index
1. 차원 축소는 왜 하는가?
2. PCA
2.0 기본컨셉
2.1 그림으로 살펴보기
2.2.선형대수학 개념 후려쳐서
2.3 코드로 살펴보기
--------------------------------
(다음 포스팅에서)
3. LDA
4. SVD
1. 차원 축소는 왜 하는가?
외출 활동이 좋은지 좋지 않은지 분류하는 머신러닝 모델을 만들고자 한다. 이를 위해 우리는 날씨 데이터를 확보했다.
지금 현재의 풍속, 온도, 습도, 미세먼지, 강수량,... 정말 많은 요인들이 영향을 미칠 것이다.
통계학에서는 이를 독립 변수라 하고, 데이터 분석/ 머신러닝에서는 이를 피쳐(Feature) 라 한다.
(본 포스팅에서는 피쳐라고 하겠음)
가령 101개의 야외활동과 관련된 항목들과 그 수치가 나열된 데이터 테이블이 있다고 한다면
| 온도 | 습도 | 강수량 | 미세먼지 | 풍속 | 태풍여부 | ... | 교통량 | 유동인구 | |
| 0801 | 32 | 15 | 66 | 3 | 111 | 0 | 15 | 40326127 | |
| 0802 | |||||||||
| ... | |||||||||
| 0831 |
하지만 위의 주어진 데이터를 그대로 학습 모델에 입력한다면, 총 101차원의 벡터일 것이다.
==> 여기서 발생하는 문제 "다중 공선성 문제"
가령 몇몇 피쳐들끼리는 강한 상관관계를 보이는 경우가 있을 것이다. (ex. 강수량과 기압)
이처럼 서로 의존성이 높은 피쳐들을 함께 학습 시키면, 모델의 과적합이 발생하여 학습 성능이 저하될 수 있음.
https://datascienceschool.net/view-notebook/36176e580d124612a376cf29872cd2f0/
따라서 모델에 해당 데이터 테이블을 때려넣기 전에 우리는
어떤 피쳐(Feature) 가 모델의 성능의 영향에 큰 영향을 줄지 파악하고,
피쳐(Feature)를 선택/가공 하는 과정을 거친다. 여기에는 총 3가지 접근 법이 있는데
1) 피쳐 선택 (Feature Selection) : 불필요한 피쳐는 버린다. 가령 야외활동 여부를 파악하는데 교통량은 크게 영향을 미치지 않는다고 가정한다면, 해당 피쳐는 버리는거다. 보통 각각의 피쳐가 모델이 야외 활동 여부를 파악하는데 영향을 미치는지 미치지 않는지 알고 싶다면
상관계수 값을 통해 판단한다.
2) 피쳐 추출 (Feature Extraction) : 피쳐들을 선택하는 것이 아니라, 더 작은 차원으로 피쳐들을 맵핑하는 것이다.
현재 101차원의 데이터 테이블을 50차원으로 압축하는 과정을 거치는 것인데, 여기에 속한 기법이 오늘 살펴볼 차원 축소 기법들
PCA, LDA, SVD, NMF 가 이다.
3) 피쳐 생성 (Feature Engineering)
이는 데이터 테이블에서 피쳐가 부족한 상황일 때 적용하는 기법으로,
해당 데이터와 만들고자하는 머신러닝 모델의 기능 활용 목적에 따라 새로운 피쳐들을 생성해 내는 것이다.
가령 우리가 야외활동 판별 여부를 알려주는 머신러닝 모델을 만들고자 하는데
해당 모델은 세렝게티 지역에 특화된 모델이라고 하자 (뜬금)
그렇다면, 해당 칼럼 중에 야외 동물 출현 횟수 같은 피쳐도 생성해줘야 하는 것이다...
2. PCA 주성분 분석 (princial component Analysis)
해당 기법을 제대로 이해하기 위해선 선형대수학 (고유벡터, 벡터 차원 등등) 키워드에 대한 이해가 필요하다.
이번 포스팅에선 최대한 수학적 개념은 배제하고 컨셉/개념이 이해되도록 설명을 해보겠다.
자세한 수학적 공식과 풀이는 포스팅의 맨 끝에 링크로 확인해보시길... (저는 그것을 설명할 재주는 없습니다...)
2.0 기본 컨셉
데이터의 피쳐를 압축하자, 데이터 테이블 매트릭스의 차원을 낮추자.
단순히 피쳐들을 빼는게 아니라,
여러개의 피쳐들이 갖는 정보를 하나로 압축 ! 하는 것임
위의 데이터 테이블을 다시 가져오면
| 온도 | 습도 | 강수량 | 미세먼지 | 풍속 | 태풍여부 | ... | 교통량 | 유동인구 | |
| 0801 | 32 | 15 | 66 | 3 | 111 | 0 | 15 | 40326127 | |
| 0802 | 0 | ||||||||
| ... | |||||||||
| 0831 |
여기 피쳐들 중 (습도 , 강수량) 혹은 (풍속, 태풍여부) 이 둘은 각각 밀접한 연관성이 있다.
습도 강수량 --> 양의 상관관계 (습도 올라가면 강수량 높음)
풍속 태풍여부 --> 양의 상관관계 (풍속 빠르면, 태풍임)
이처럼 연관성이 높은 피쳐들을 하나로 합쳐주는 작업이 주성분 분석이 된다.
해당 데이터 피쳐들은 쉽고 직관적이기 때문에 어떤 것끼리 합치면 좋을지 감(?) 이 오는데
당최 알 수 없는 수치들의 나열인 데이터 테이블을 받았다고 했을 때 (뭐 인공위성의 궤도, 신호1, 신호2, 등등)
우리는 어떻게 여러 개의 피쳐를 하나의 피쳐로 줄일 수 있을까?
이때 하는 것이 주성분 분석 (Principal component Analysis) 이다.
2.1 쉽게 그림으로 살펴보기
(해당 이미지 자료들은 유투브 설명영상에서 캡쳐한 것이며, 출처는 사진 밑 그리고 포스팅 밑에 적어두었습니다.)

가령 우리에게는 아래와 같은 2차원 공간에 데이터들이 있다.
우리의 목표는 이 2차원 공간의 데이터를 1차원 공간의 데이터로 만들어 주는 것이다
==> 차원 축소의 기본적인 컨셉 여기에서 우리가 할수 있는 방법은 2가지 인데
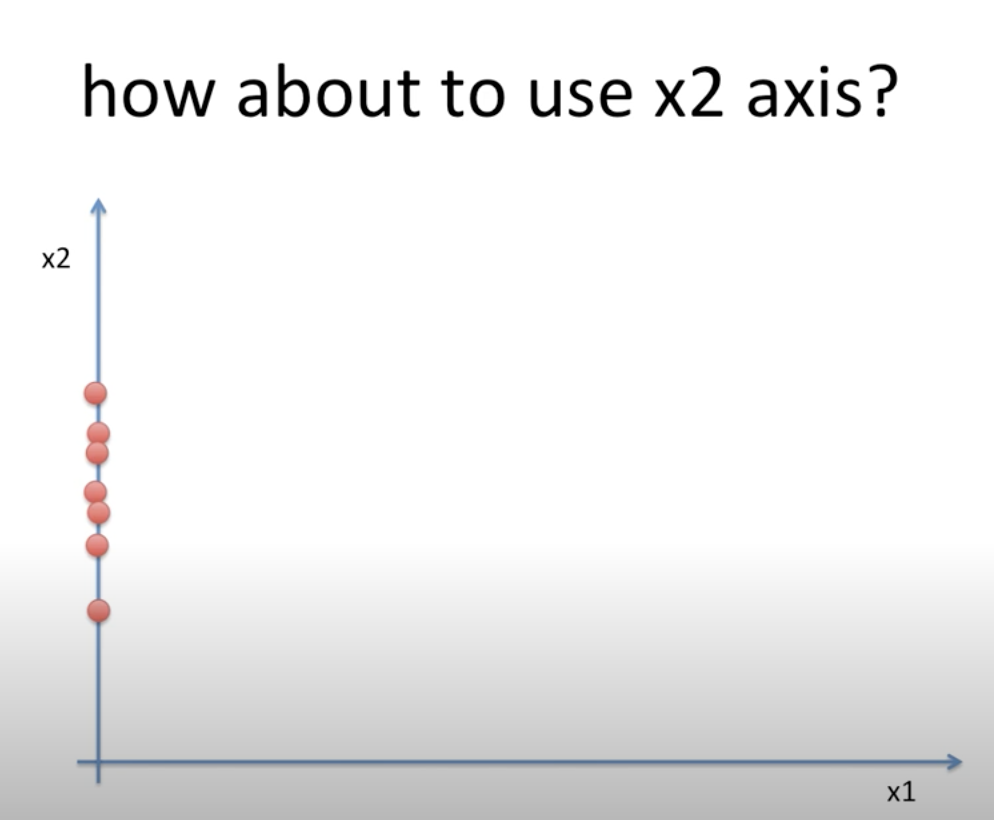
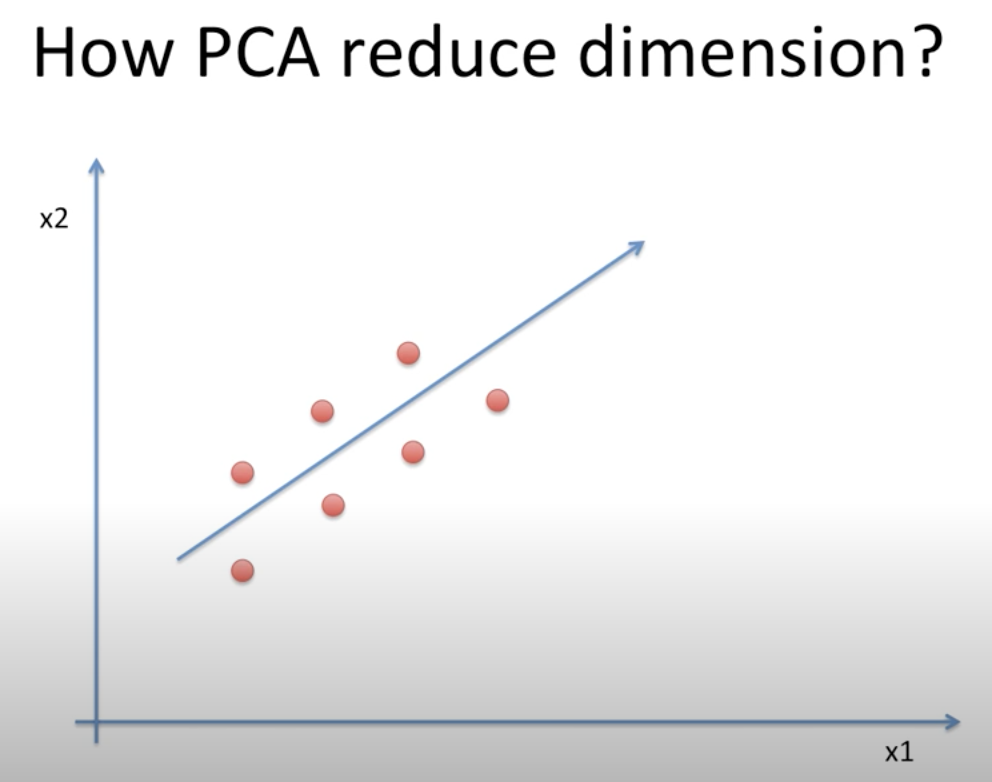
| 방법 1. 냅다 내려버리기 | 방법 2. 새로운 차원 찾기 |
  |
 |
방법1 에서는 차원 x1, x2 에 냅다 데이터를 내려버렸다.
이렇게 할 경우 문제점은 내린 후에 값이 겹치는 데이터들이 많고, 아예 한 차원의 정보는 유실되게 된다.
반면 방법2에서는 새로운 차원 (화살표) 에 데이터들을 내려줬다.
이렇게 한 결과 데이터들은 방법1에서의 문제를 어느정도 해결하게 된다.
여기서 중요한 것은 데이터들이 겹치지 않게 끔하는 화살표를 찾는 것!!!!
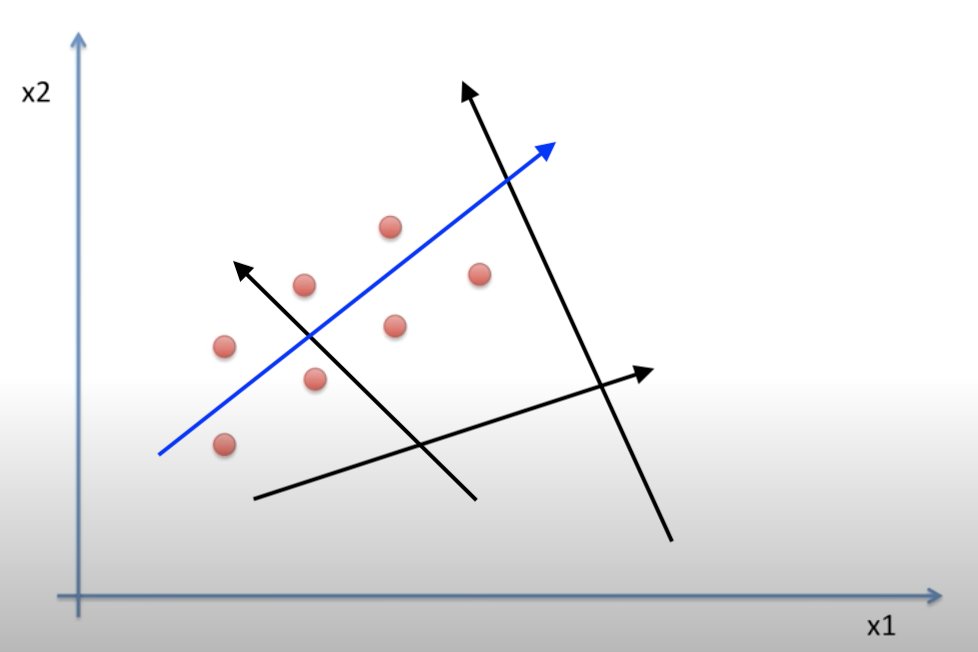 |
 |
좌측에 사진처럼 2차원 상에서 무수히 다양한 화살표를 그릴 수 있다.
하지만 우리는 그 중 파란색 화살표 처럼
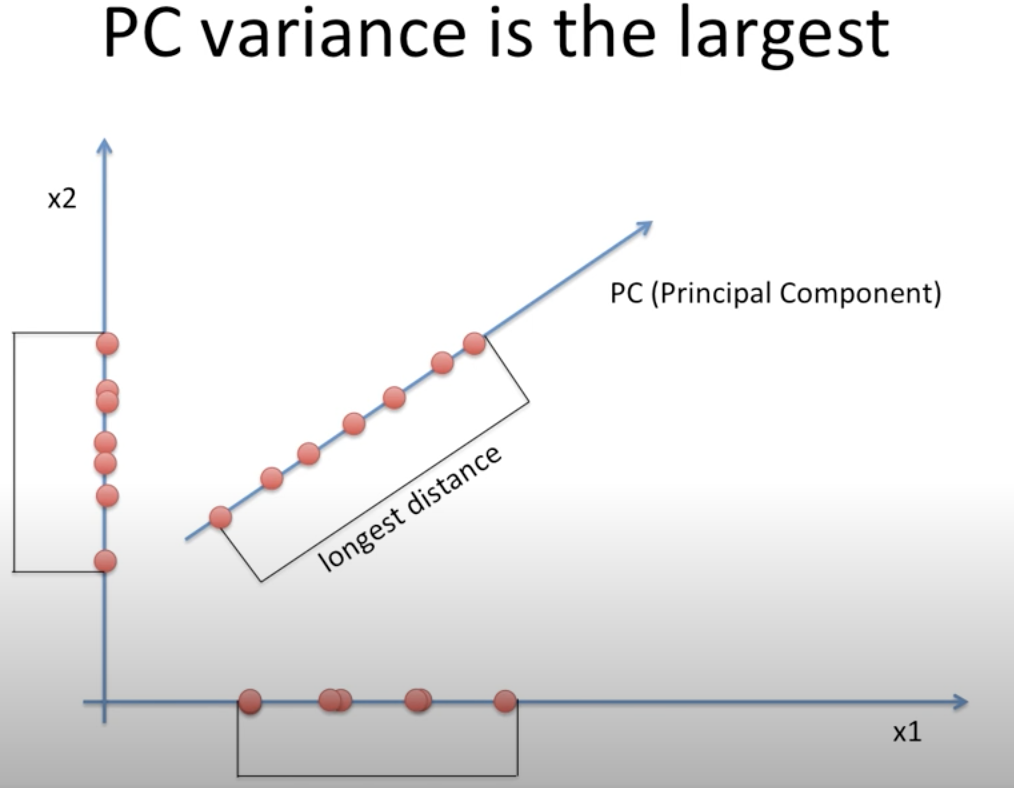
데이터를 해당 화살표에 1차원 으로 내렸을 때 겹치지 않게 하는 화살표를 찾아야 한다. (longest distance)
==> 정리하자면
1) 수많은 화살표 들 중, 데이터 들을 화살표에 내렸을 때, 데이터가 최대한 안 겹치게, 멀리 퍼지게 하는 길이가 긴 화살표 찾기
2) 거기에 데이터들을 투영
3) (2차원 이상의 경우 2차원으로 만들고자 한다면)
만약 또 하나의 화살표 만들 때 축 끼리는 직각이 되어야 함, 최대한 데이터가 겹치지 않도록
==> 이걸 선형대수학에서의 워딩으로 해석하자면
1) 공분산 행렬에서 고유 벡터/고유값을 구하고
2) 가장 분산이 큰 방향을 가진 고유벡터(e1) 에 입력데이터를 선형변환
3) 고유벡터(e1) 과 직교하며, e1 다음으로 분산이 큰 e2 고유벡터에 또 선형변환.
(울지말자... 최대한 쉽게.. 이해해보자....)
2.2 선형대수학 개념들 후려쳐서 이해하기
* 공분산 : 한 변수간의 변동을 분산, 두 변수 간의 변동은 공분산
* 고유 벡터: (화살표) 행렬X에 다른 행렬A를 곱했을때, 행렬X의 벡터들 중 벡터의 크기는 변하지만, 방향은 변하지 않는 벡터
* 고유값 : 해당 고유 벡터의 크기 (화살표의 길이)
* 선형변환 행렬X 에 다른 행렬A 를 곱해줌으로써 공간 A에 행렬X 를 맵핑(mapping, 투영/사상이라고도함) 시켜주는 개념.
1 > " 공분산 행렬은 대칭행렬이다. "

한 변수 간의 변동을 분산, 두 변수 간의 변동은 공분산 이라고 한다.
우리는 변수 x1,x2,x3 에 대해 각각의 분산, 공분산을 행렬로 표현할 수 있고 이를 공분산 행렬이라 한다.
공분산 행렬은 대각 성분에는 자기 자신 (x1,x1) 의 분산이며 나머지 성분은 서로 다른 두 변수간의 변동 즉 공분산 값이다.
여기서 중요한 것은 행렬의 1,2 성분 ( (x1,x2 간의 공분산) 과 행렬의 2,1 성분 (x2,x1간의 공분산)은 같을 수 밖에 없음
따라서 해당 행렬은 n,k 성분과 k,n 성분이 같은 대칭행렬 !
2 > "대칭 행렬에서는 고유벡터를 직교 행렬로, 고유값을 정방행렬로 대각화 할 수 있다"
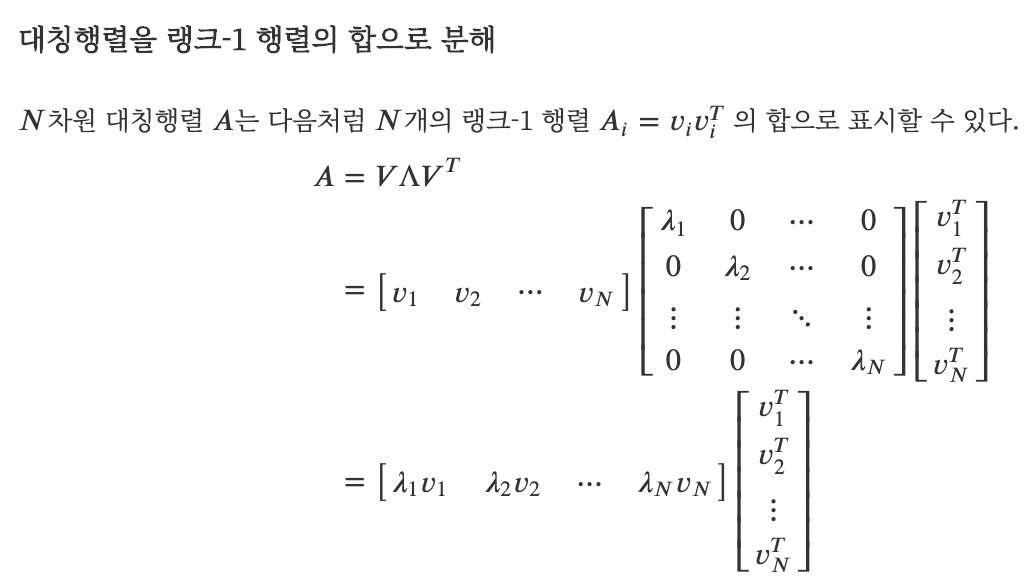
공분산행렬은 대칭행렬이기 때문에 고유값 분해를 했을 때,
고유백터의 직교 행렬(V) * 고유값의 정방행렬 ∧ * 고유 벡터의 직교 행렬의 전지행렬 (VT) 로 표현된다.
이때 v1 은 가장 분산이 큰 방향을 가진 고유벡터이며,
v2는 v1 에 직교하면서, 다음으로 가장 분산이 큰 방향을 가진 고유벡터가 된다.
=> 즉 고유백터들이 아까 우리가 그토록 찾던 ! 가장 분산이 큰 화살표 들인거다.
자세한 설명은
https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
https://datascienceschool.net/view-notebook/7fd58178d9e64be682058db7e024d8b5/
결국 정리하자면,
( 만약 내가 400차원 데이터를 k 차원으로 줄이고자 한다 )
1. 입력 데이터의 공분산 행렬을 구한다.
2. 공분산 행렬을 고유값 분해 해서 고유 벡터와 고유값을 구한다 (앞서 말한 최고의 화살표찾기)
3. 고유값이 가장 큰 (화살표 길이가 가장 긴) k개의 고유 벡터를 추출
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 입력 데이터들을 선형 변환
2.3 코드로 구현
참고 : 파이썬 머신러닝 완벽 가이드
아이리스 데이터를 활용할 것이고, 해당 데이터의 4가지 피쳐를 주성분 분석을 통해 2가치 피쳐로 줄여볼 생각!
1) 데이터 로드
from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# 사이킷런 내장 데이터 셋 API 호출
iris = load_iris()
# 넘파이 데이터 셋을 Pandas DataFrame으로 변환
columns = ['sepal_length','sepal_width','petal_length','petal_width']
irisDF = pd.DataFrame(iris.data , columns=columns)
irisDF['target']=iris.target
irisDF.head(3)
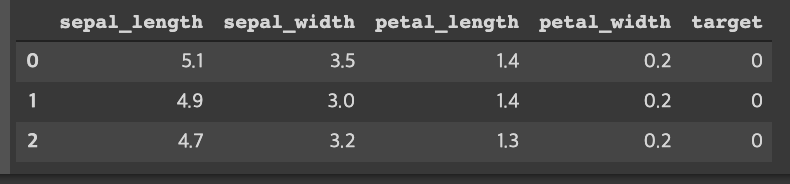
해당 데이터는'sepal_length','sepal_width','petal_length','petal_width' 4가지 피쳐로 된 데이터이고,
target 값은 붓꽃의 종류 setosa, versicolor, virginica 세가지 이고, 각각 0/ 1 / 2 로 라벨 인코딩되었다.
2) 각 클래스별 데이터 분포 시각화
#setosa는 세모, versicolor는 네모, virginica는 동그라미로 표현
markers=['^', 's', 'o']
#setosa의 target 값은 0, versicolor는 1, virginica는 2. 각 target 별로 다른 shape으로 scatter plot
for i, marker in enumerate(markers):
x_axis_data = irisDF[irisDF['target']==i]['sepal_length']
y_axis_data = irisDF[irisDF['target']==i]['sepal_width']
plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])
plt.legend()
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.show()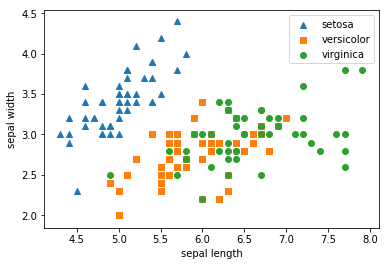
네가지 피쳐 중 두가지 피쳐 sepal width / sepal length 를 활용해서 각 클래스 별 데이터 분포가 어떻게 되어있는지 확인했다.
두 피쳐를 활용해 setosa는 명확히 구분해 낼 수 있지만, versicolor와 virginica 는 구분하기 어렵다.
3) 각 칼럼별 데이터 표준화
# 주성분 분석 전에 표준화 (평균0, 편차 1의 표준정규분포로 각 칼럼데이터 표준화시키기)
from sklearn.preprocessing import StandardScaler
irisDF_inputs = irisDF.iloc[:,:4] # 타겟 값을 제외한 피쳐만 추출
iris_scaled = StandardScaler().fit_transform(irisDF_inputs)
iris_scale_DF = pd.DataFrame(iris_scaled)
iris_scale_DF['target'] = irisDF.target
iris_scale_DF.describe()
우선 해당 데이터 칼럼들의 주성분 분석을 하기 전에 각 칼럼별 데이터를 표준화 시켜줘야한다.
데이터 표준화에 대한 자세한 설명은 해당 포스팅을 참고! (https://huidea.tistory.com/39)
표준화 한후 각 칼럼별 데이터의 평균, 편차를 살펴보자면,
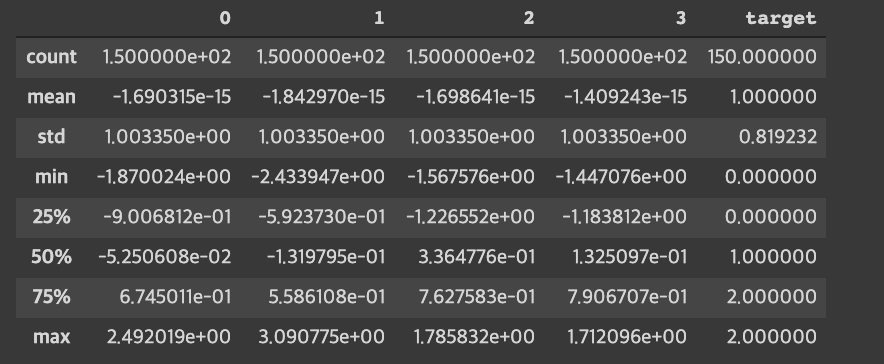
4) 표준화 이후 주성분 분석 (피쳐 4개에서 2개로 줄이기)
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# 표준화 시켜줌
iris_scaled = StandardScaler().fit_transform(irisDF)
# 주성분 분석 !
pca = PCA(n_components=2) # n_components 몇개의 피쳐로 데이터 차원 줄일건지
# fit( )과 transform( ) 을 호출하여 PCA 변환 데이터 반환
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
# PCA 환된 데이터의 컬럼명을 각각 pca_component_1, pca_component_2로 명명
pca_columns=['pca_component_1','pca_component_2']
irisDF_pca = pd.DataFrame(iris_pca,columns=pca_columns)
irisDF_pca['target']=iris.target
display(irisDF_pca.head(3))
# 주성분 분석 이후 평균/표준편차 확인
display(irisDF_pca.describe())

차원을 축소한 후 피쳐 4개가 피쳐 2개로 줄어든 것을 확인 할 수 있다.
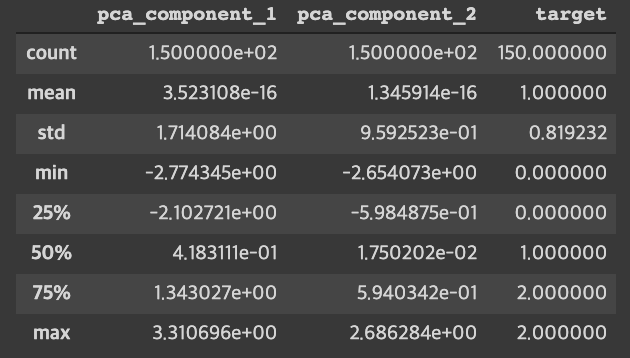
각 피쳐들의 평균, 표준편차도 확인해보면, 앞의 4가지 피쳐들의 값과는 달라진 것을 확인 가능.
5) 주성분 분석 결과 시각화
#setosa를 세모, versicolor를 네모, virginica를 동그라미로 표시
markers=['^', 's', 'o']
#pca_component_1 을 x축, pc_component_2를 y축으로 scatter plot 수행.
for i, marker in enumerate(markers):
x_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_1']
y_axis_data = irisDF_pca[irisDF_pca['target']==i]['pca_component_2']
plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])
plt.legend()
plt.xlabel('pca_component_1')
plt.ylabel('pca_component_2')
plt.show()
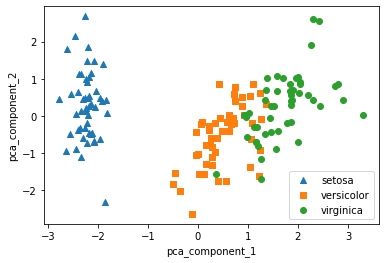
두 개의 피쳐만으로도 세가지 클래스가 대략 분류 되는 것을 확인 할 수 있음
다음에는 LDA 와 SVD 를 살펴보겠다.
참고한 자료 링크 :
책 : 파이썬 머신러닝 완벽 가이드
영상 설명 :
https://www.youtube.com/watch?v=jNwf-JUGWgg&t=1034s
https://www.youtube.com/watch?v=xebPVQ1f7nM&t=273s
수학 개념 설명 잘되어있음 !
https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
고유값 분해 코드로 구현까지!
https://datascienceschool.net/view-notebook/7fd58178d9e64be682058db7e024d8b5/
+) 사실 공분산 행렬에서 고유벡터, 고유값 추출하는 부분 (최적의 화살표 찾는 부분) 은
고유값 분해 설명이 조금 자세히 들어가야해서, 이 포스팅에서는 설명하지 않고 관련 링크를 달았다.
수학을 더 잘하게 될 미래의 내가 추후보완하길 바라며...




댓글