[Machine learning] PCA(주성분분석), LDA(선형판별분석법), SVD (행렬분해) (쉽게 설명하는 차원 축소 기법들 총정리 part2)

(이전 포스팅)

https://huidea.tistory.com/44?category=879541

[Machine learning] PCA 주성분분석 (쉽게 설명하는 차원 축소 기법들 총정리 part1) 200803

 

Index 

1. 차원 축소는 왜 하는가?

2. PCA

 

(이번 포스팅은 여기서 부터 ) 

3. LDA  

4. SVD

 

 

3. LDA (Linear Discriminant Analysis) 선형판별분석법 

Q. 구글에 LDA 를 검색하면 두개가 나오는데? 

LDA 는 토픽모델링(Topic Modeling) 기법 가운데 하나인 

잠재디리클레할당(Latent Dirichlet Allocation, LDA)와 이니셜이 같아서 헷갈리는데 

이번 포스팅에서 다룰 SVD (행렬분해)를 자연어처리 토픽 모델링에 적용한게 잠재디리클레할당(Latent Dirichlet Allocation, LDA)고, 

지금 3장에서 다룰 LDA (Linear Discriminant Analysis)는 저번에 다룬 PCA 에서 확장된 차원 축소 기법이다. 

 

정리 하자면, 

LDA (Linear Discriminant Analysis) : PCA 와 유사한 차원축소 기법 

 

잠재디리클레할당(Latent Dirichlet Allocation, LDA):

자연어 처리에서 문서별 토픽 건지는데 쓰는 기법, SVD 차원축소 자연어에 적용한 기법

 

3.0. 기본 컨셉 

 

# 클래스가 있는 지도 학습에서 사용 

LDA 기법은 지도 학습(supervised - learning)에서 적용하는 차원 축소 기법

 

지도 학습의 가장 중요한 핵심은 데이터의 class 가 있다는 것, 클래스(Class) 는 모델이 맞춰야 할 정답을 의미

가령 우리가 붓꽃의 종류 3가지를 분류하는 모델을 현재 만든다고 하면 붓꽃 종류가 해당 모델의 클래스

지도 학습에서는 데이터의 피쳐(=붓꽃의 특징)와 정답(=붓꽃의 종류)을 통해 학습을 진행(=붓꽃 특징 기반 종류 분류 모델) 

 

 

 

# PCA 랑 차이점은 

이전에 살펴본 PCA 데이터의 차원을 줄이기 위해, 주어진 데이터가 최대한 안겹치게 내려질 수 있는 화살표를 찾았다.  

선형 대수 워딩으로 바꾸면, 각 피쳐별 공분산 행렬을 활용해 데이터의 변동성이 가장 큰 축을 찾는 것이었다. 

 

반면, LDA는 입력 데이터의 클래스(정답) 를 최대한 분리할 수 있는 축을 찾는다. 

 

 

위의 그림에서 보듯이 데이터가 점으로 표현되어있고, 밑의 축을 통해 2차원의 데이터가 1차원 직선으로 투영되고 있음.

좌측의 그림보다 우측의 그림에서 빨강 /파랑 이 보다 명확히 분류 되는 것을 확인

우측의 그림처럼 클래스 (빨파) 가 명확히 분류되게 하는 축을 찾는게 LDA 의 목표

 

즉 다른 말로 하자면, 특정 공간상에서 클래스 분리를 최대화 하는 축을 찾는 것 

이를 위해 클래스 간 분산 을 최대화 하고 클래스 내부 분산을 최소화 하는 방식으로 차원을 축소한다. 

 

아래 그림에서 1번 화살표의 길이는 크게, 2번 화살표의 길이는 작게 만드는 컨셉!

그럼 어떻게 클래스 간 분산과 클래스 내부 분산을 구하남? 바로 클래스별 산포 행렬을 활용한다. 

 

 

3.1. 클래스 산포 행렬

1) 클래스 간 분산, 2)클래스 내부 분산 행렬 두 행렬을 생성한 뒤에, 이 산포 행렬들을 기반으로 고유 벡터를 구함

공식은 다음과 같다.

 

 

 

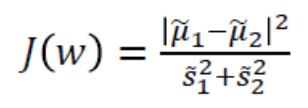3.2. 코드 구현 

참고 : 파이썬 머신러닝 완벽 가이드 

 

1) 오늘도 아이리스 데이터를 불러옵니당

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
import pandas as pd

# 데이터 불러오기 
iris = load_iris()

# 표준화 작업
iris_scaled = StandardScaler().fit_transform(iris.data)

# dataframe 으로 바꿔서 데이터 형태 보기 
iris_df = pd.DataFrame(iris_scaled)
display(iris_df.head(10))

 

* 표준화 작업 거침. 표준화 설명은 요기!

[Machine learning] 데이터 표준화, 정규화, 피쳐스케일링 - 200729

 

2) LDA 적용 ! 원래 4차원으로 구성되어있던 값을 2차원으로 축소 

lda = LinearDiscriminantAnalysis(n_components=2) # LDA 적용, 2차원으로 줄이기 설정
lda.fit(iris_scaled, iris.target)
iris_lda = lda.transform(iris_scaled)

print("BEFORE",iris_scaled[:10])
print("BEFORE SHAPE",iris_scaled.shape)

print()

print("AFTER",iris_lda[:10])
print("AFTER SHAPE",iris_lda.shape)

* 전후 비교 (각 데이터 10행까지만 출력했음! 실제는 shape 에서 보듯이 150행 까지 있음) 

 

 

 

3) 시각화해서 보기 

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

lda_columns=['lda_component_1','lda_component_2']
irisDF_lda = pd.DataFrame(iris_lda,columns=lda_columns)
irisDF_lda['target']=iris.target

#setosa는 세모, versicolor는 네모, virginica는 동그라미로 표현
markers=['^', 's', 'o']

#setosa의 target 값은 0, versicolor는 1, virginica는 2. 각 target 별로 다른 shape으로 scatter plot
for i, marker in enumerate(markers):
    x_axis_data = irisDF_lda[irisDF_lda['target']==i]['lda_component_1']
    y_axis_data = irisDF_lda[irisDF_lda['target']==i]['lda_component_2']

    plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])

plt.legend(loc='upper right')
plt.xlabel('lda_component_1')
plt.ylabel('lda_component_2')
plt.show()

 

4.  SVD 특이값 분해 

대부분의 자료는 아래의 링크에서 가져왔으며,

아래 설명은 제 개인 공부를 위해 링크 내용들을 정리한 것이니 제대로 수식까지 깊게 이해하고 싶다면 아래의 링크로...! 

https://www.youtube.com/watch?v=cq5qlYtnLoY&t=520s

https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/

https://angeloyeo.github.io/2019/08/01/SVD.html

 

4.0. 기본 컨셉 

# PCA에서는 고유값 분해, SVD는 특이값 분해? 

PCA와 같은 행렬 분해 기법이지만, PCA는 n*n 형태의 정사각행렬 일때 고유값 분해를 할 수 있다. 

 

따라서 우리는 PCA에서 데이터를 n*n 형태의 공분산 행렬로 만들었고,

이를 활용해 고유값을 추출하는게 (가장 큰 분산을 보이는 축을 찾는게) PCA 의 목적이었다. 

 

반면 SVD는 정사각행렬이 아닌 m*n 형태의 다양한 행렬을 분해하며, 이를 특이값 분해라 말한다. 

이때 분해되는 행렬은 두 개의 직교 행렬과 하나의 대각행렬이며, 두 직교행렬에 담긴 벡터가 특이벡터다. 

출처 : https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/

 

A : m×n 직사각 행렬 (rectangular matrix ) 
U : m×m 직교 행렬 (orthogonal matrix)
Σ : m×n 대각행렬 (diagonal matrix) - 대각성분 (1,1) (2,2)... 만 값이 있고 나머지들은 다 0
V : n×n 직교 행렬 (orthogonal matrix) 

 

    +) 직교행렬 :

U가 직교행렬이 되려면, U와 U의 전치행렬을 내적한 것이 단위행렬이 되어야한다.

근데 내적해서 단위행렬이 튀어나오는 두 행렬은 역의 관계가 아닌가, 따라서 아래와 같은 식이 성립되면 직교행렬이다.

https://www.youtube.com/watch?v=cq5qlYtnLoY&t=520s

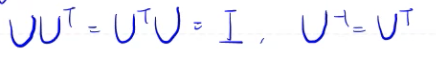
근데 차원을 축소하겠다면서 왜 뜬금없이, 직교행렬 두 개, 대각행렬 하나를 뚝딱 만드는가?

이게 무슨 의미가 있나? 

(대부분 https://angeloyeo.github.io/2019/08/01/SVD.html  이 링크 내용 가져옴.. 정말 설명 잘되어있당..) 

 

# 특이값 분해의 기하학적 의미 

 

특이값 분해에서 묻는 근본적인 질문은 아래와 같다. 

" 특정 직교 행렬(X) 을 선형 변환 할텐데 해당 직교 행렬(X) 안에서의 특정 두 벡터(x1,x2)가 직교한다면

선형 변환한 이후 (u1,u2) 에도 벡터의 크기는 변하지만, 여전히 직교하는가? "

이게 뭔소리인가. 

 

 

아래의 그림을 보자면, 

아래의 그림에서 x 하나의 직교 행렬이고, Ax 는  x라는 직교 행렬에 선형변환한 행렬이다. 

즉, 초록색 점(x벡터)가 선형 변환된 벡터 값이 파란색 점(Ax)벡터임

이 과정이 연속적으로 진행되어서 원을 그리는 형상으로 아래에서 시각화 됨

 

이때 우측의 그림을 살펴보면 원래의 데이터 행렬(초록색)에서 직각이 되는 두 벡터가 있는데, 

그때 동시에 선형변환된 행렬에서도 직각(파란색) 이 되는 두 벡터가 있다. 

 

==> 바로 이때 !!! ( 이 두가지 경우 말고도 또 있을 것임) 

 

그럼 다시 아까 특이값 분해의 공식으로 돌아가보자면,

 

출처 : https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/

여기서 초기의 직교행렬은 (x1,x2가 돌아다니는 원) 는  V 고, 

선형 변환시킨 직교행렬은 (Ax1, Ax2 가돌아다니는 원) 는 U 다. 

그리고 여기서 시그마는 singular value(즉, scaling factor) 가 된다.

 

즉, 우리는 선형 변환을 통해 (A라는 행렬을 원래의 매트릭스에 곱해주는 행위) AV = UΣ 를 만들었다.

이때 아까 앞서 던졌던 질문처럼 " V에서 직교할때, A행렬로 선형 변환한 행렬 U에서도 직교하는가" 를 해석해야한다

.

AV = UΣ 식은 앞서 말한 직교 행렬의 특성들을 활용해서 (V와 V 의 전치를 내적하면 단위, V와 V 의 전치는 역행렬관계)

AV(V)t = UΣ(V)t 

A =  UΣ(V)t  이 공식으로 오게 된다. 

https://angeloyeo.github.io/2019/08/01/SVD.html

이 공식은 다시 이렇게 풀어 쓸 수 있는데 여기서 u1*(v1)t 는 하나의 매트릭스가 되고, 시그마1이 스칼라 값이다. 

따라서 un*(vn)t 각각의 매트릭스 크기들은 그 앞에 곱해지는 각각의 시그마 값에 의해 결정되게 된다. 

시그마는 여기서 각 매트릭스의 정보량을 의미하게 된다.

 

 

https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-20-%ED%8A%B9%EC%9D%B4%EA%B0%92-%EB%B6%84%ED%95%B4Singular-Value-Decomposition

https://www.youtube.com/watch?v=cq5qlYtnLoY