https://huidea.tistory.com/246
[Machine learning] 선형회귀모델 (1) 모델검정 - 정규성/등분산성/독립성
Intro. 선형회귀 모델을 구현할 때, 그저 LinearRegression.fit()을 해도 학습은 물론 된다. 하지만, 생성된 모델이 선형회귀의 기본 가정을 따르는지 아닌지 체크가 필요하다. 선형회귀가정에 따르지도
huidea.tistory.com
이 포스팅에 이어 이번 포스팅에서는 선형회귀모델의 결과 해석에 대해 살펴보고자 한다.
index
1. Boston 집값 예측으로 모델링
2. Stats model summary 의미 해석
3. R2score의 의미
1. Boston 집값 예측으로 모델링
#### 0. import module ####
from sklearn.datasets import load_boston
import numpy as np
import pandas as pd
import scipy as sp
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
#### 1. data load & split ####
def data_load_split():
### 1) data load
boston = load_boston()
### 2) setting X, Y variable
X = pd.DataFrame(boston.data, columns = boston.feature_names)
Y = pd.DataFrame(boston.target, columns = ['MEDV'])
### 3) train, test data split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 2022)
return X, Y, X_train, X_test, y_train, y_test
X, Y, X_train, X_test, y_train, y_test = data_load_split()
#### 2. modeling ####
X_train = sm.add_constant(X_train) ### 선형 회귀 식의 beta 0를 만드는 과정
model = sm.OLS(y_train, X_train, axis = 1) ## OLS data modeling
model_trained = model.fit() ## 모델 fitting
model_residuals = model_trained.resid ### 모델의 잔차(예측값 - 타겟값)
우선 퀵하게 데이터 불러와서 모델을 만들었다. (EDA, 선형회귀모델 가정 검정과정 생략)
OLS는 statsmodel 패키지에서 최소자승법으로 만들어진 linear regression 모델이다.
코드 전체 풀버전은 아래 깃헙링크 참고 !
2. Stats model summary 의미 해석
print(model_trained.summary())

위 코드를 입력하면, 아래와 같은 summary가 나온다.
선형회귀 summary는 sklearn linearregression 에서는 제공하지 않고
Statsmodels 패키지의 linearregression 모델에게만 제공한다.
0) 귀무가설 : X(독립변수)의 계수(b1)가 0이다
1) coef : 각 변수별 계수 추정치
2) 피쳐 들 중 첫번째 const : y절편 (beta0)
3) std err : 계수 추정치의 표준편차
4) t : t검정 통계량 값

→ 즉, t값이 크면 추정된 계수가 0이 아니라는 것
→ 귀무가설 (X(독립변수)의 계수(b1)가 0이다) 기각
5) pvalue가 0.1보다 큰 경우 귀무가설 통과
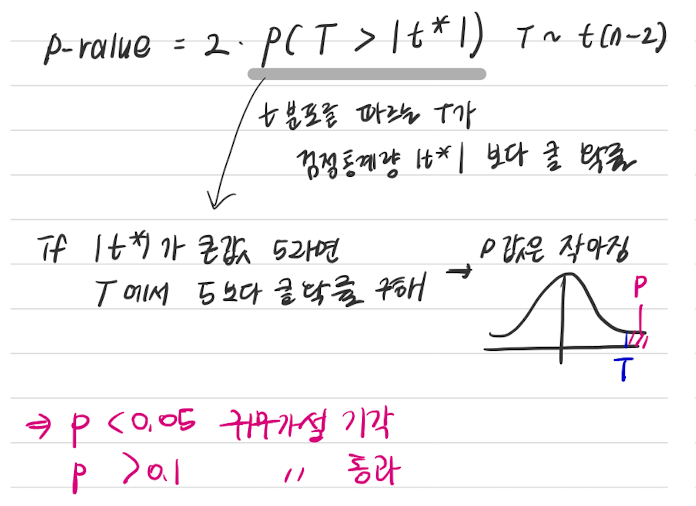
→ 여기서 귀무가설은 "X(독립변수)의 계수(b1)가 0이다"
→ 즉 pvalue가 0.1보다 큰 독립변수의 계수는 0이다.
→ age, indus 피쳐는 유의하지 않다고 해석가능 → 해당 피쳐는 제외하고 모델 재설계 해야함.
3. R2 score
위에서 r2 score는 0.756, 무슨의미?


SSR : Y의 평균값과 예측값의 차 제곱
SST : Y의 평균값과 실제값의 차 제곱
R2 score는 0~1사이의 값
1) R2 score (SSR / SST) = 1 은
예측값과 실제값이 같다는 의미, 예측 아주 잘됨 ~!
→ (통계적으로 표현) 독립변수로 종속변수를 추정했는데 실제값과 같음, 독립변수 효과 있음
2) R2 score (SSR / SST) = 0은
분자인 SSR가 0, 즉 예측값이 평균값과 같다는 것.. 예측을 그냥 평균으로 때려맞춤, 예측 개판ㅠㅠ
→ (통계적으로 표현) 독립변수로 종속변수를 추정했는데 평균값과 같음, 독립변수 효과 전혀 없음
즉, R2 score 는 독립변수가 종속변수 추정에 얼마나 효과가 있는지 판단하는 척도로 쓰임

위와 같이 표현을 함
참고 link : https://www.youtube.com/watch?v=ClKeKeNz7RM&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=26




댓글