intro.
로지스틱 회귀모델이 이름만 회귀지 "분류" 모델인 것은 머신러닝 입문자라면 쉽게 알 수 있다.
이번 시간에는 어떤 수식/가정을 통해서 연산이 되는지 살펴보고
그 다음 포스팅에서는 직접 데이터에 적용해보며 로지스틱 회귀 분석에서의 유의 사항을 살펴보겠다.
핵심 참고 내용은 김성범 교수님 핵심 머신러닝의 로지스틱 회귀모델 강의다.
1편 : https://www.youtube.com/watch?v=l_8XEj2_9rk&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=25
2편 : https://www.youtube.com/watch?v=Vh_7QttroGM&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=24
index
1. 로지스틱 회귀분석
2. 로지스틱 회귀의 Y값은 베르누이 분포를 따른다.
3. 로지스틱 회귀의 가정 "에러의 평균은 0이다.
4. 로지스틱 함수를 적용
5. 승산
6. 파라미터 추정 - MLE
7. 결과 및 해석
1. 로지스틱 회귀분석
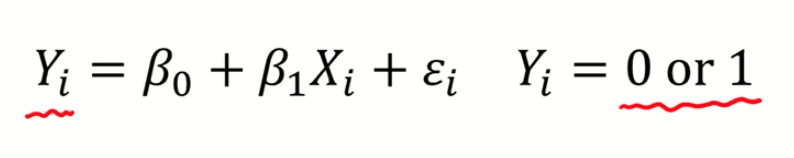
# 컨셉 :
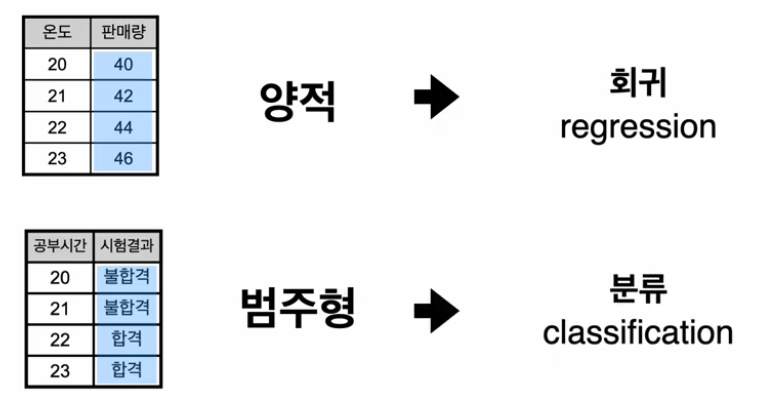
로지스틱 회귀 분석은 이름에는 회귀가 들어갔지만, 분류 모델이다.
기존 선형회귀는 연속형 수치를 (ex. 판매량, 나이, 집값, 연봉 등) 예측하는게 목표였다면
로지스틱 회귀 분석은 범주형 값을 (ex. 합격/불합격, 남/여) 을 예측하는게 목표다.
# 선형 회귀와 가장 큰 차이점 : Y 값이 0 또는 1인 값 즉, "Y 값이 정규분포가 아니다"

- 선형회귀의 대전제 : "확률오차가 정규분포를 따른다"
→ 위 전제를 바탕으로 " Y 값도 정규분포를 따른다"
→ 위 전제를 바탕으로 파라미터 값 LSE(최소제곱법)으로 추정
하지만 로지스틱 회귀에서는 범주형 분류기 때문에 Y 값이 정규분포를 따르지 않음
- 대신 로지스틱에서의 범주형 Y 값은 정규 분포가 아니라 "베르누이 분포" 형태를 띈다 !!
2. 로지스틱 회귀의 Y값은 베르누이 분포를 따른다.

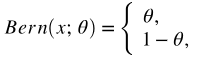
# 베르누이 시행 :
결과가 두 가지 중 하나로만 나오는 실험이나 시행을 베르누이 시행(Bernoulli trial)
예를 들어 동전을 한 번 던져 앞면(H:Head)이 나오거나 뒷면(T:Tail)이 나오게 하는 것도 베르누이 시행
# 베르누이 확률 변수 :
베르누이 시행의 결과를 실수 0 또는 1로 바꾼 것을 **베르누이 확률변수(Bernoulli random variable)
베르누이 확률변수는 두 값 중 하나만 가질 수 있으므로 이산확률변수(discrete random variable)
베르누이 확률변수의 표본값은 보통 정수 1과 0으로 표현하지만 때로는 정수 1과 -1로 표현하는 경우도 있음
# 베르누이 확률 분포 *** :

x 가 1일 때 확률이 파이면 나머지 x가 0일때 확률은 1-파이다.

그리고 베르누이 분포에서 1이 나올 확률을 의미하는 파이는(µ) 모수(parameter)를 가진다.
변수와 모수는 세미콜론 기호로 분리해서 표기한다.
+) 여기서 잠깐 모수를 가진다는게 무슨 의미인가?
모수는 우리가 알 수 없고 표본의 대표값을 통해 추정하는 모집단의 대표값을 의미한다.
파이는(µ)는 x가 1일 확률을 의미하므로 고정된 값이 아니라 모집단에서 나온 표본의 값이다.
# 베르누이 확률 변수의 기댓값 (평균값) : 파이(µ)
+) 기댓값 : (각 사건이 벌어졌을 때의 이득 * 그 사건이 벌어질 확률) -> 이걸 전체 사건에 대해 합한 것
주사위의 기댓값은

따라서, 베르누이 확률 변수에서 기댓값은 파이(µ) 다.

→ 1 * µi (= yi 가 1일때) + 0 * (1-µi) (= yi 가 0일때)
3. 로지스틱 회귀의 가정 "에러의 평균은 0이다."
# 가정 : 에러의 평균이 0이다.

에러의 평균이 0 이면, 로지스틱 회귀에서 Y의 기댓값은 β0 + β1Xi 가 된다.
그럼 위의 2번에서 도출한 내용과 합쳐 보자면,

Q. 여기까진 알겠음. 근데 우리가 알고있는 β0 + β1Xi 의 함수 형태는 선형의 형태가 아닌가?
결과 값은 0 또는 1어야 하는데, 이 형태가 적합한가?
A. ㄴㄴ S 커브 형태의 함수식으로 바꿔보자
4. 로지스틱 함수를 적용
4.1. S 커브 함수가 필요하다 !
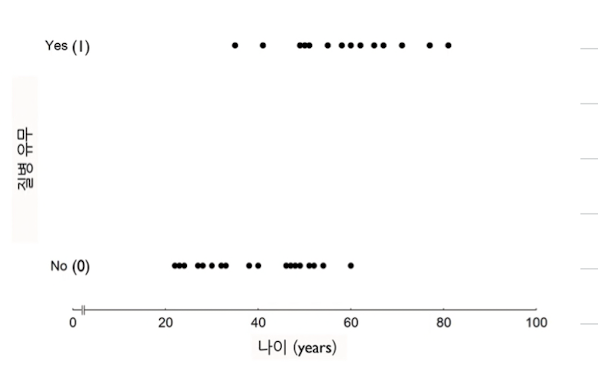

* 범주형 예측에서는 좌측 선형으로 표현이 안됨, 따라서 우측과 같이 S커브의 형태를 띄는 함수를 가져다 써야함
* 로지스틱 회귀 모델에서는 로지스틱 함수 형태를 씀 !

+) 시그모이드 함수 개념안에 로지스틱 함수가 속한 것
시그모이드 함수는 S커브 형태를 띄며 미분가능하다는 특징을 가지고 있음
이 시그모이드 함수안에 속한 것이 로지스틱함수, 쌍곡탄젠트 함수, 오차함수 등이 있다.

4.2. 목차 3에서 찾아낸 함수의 기댓값에 로지스틱 회귀 모델을 씌워보면?


기존 선형 결합의 형태였던 β0 + β1Xi 에서 로지스틱 함수를 씌워서 S커브로 바꿈
이제 위 식에서의 파라미터 추정(β0, β1) 을 해보자.
하지만 위의 식은 Exponential 함수 때문에 β0 , β1 계산이 쉽지 않아보인다.
이때 승산(odds) !!! 의 개념을 적용하면 연산이 조금 쉬워진다 !
따라서 β0 , β1 추정하기전 승산의 개념을 먼저 살펴보자면,
5. 승산 (odd)
1) 승산 (odds)
: 성공 확률을 p로 정의할 때, 실패 대비 성공 확률의 비율

a. 이 로지스틱 회귀로 승산을 구해보자면?

b. 위 odds 식에 로그를 씌워보자
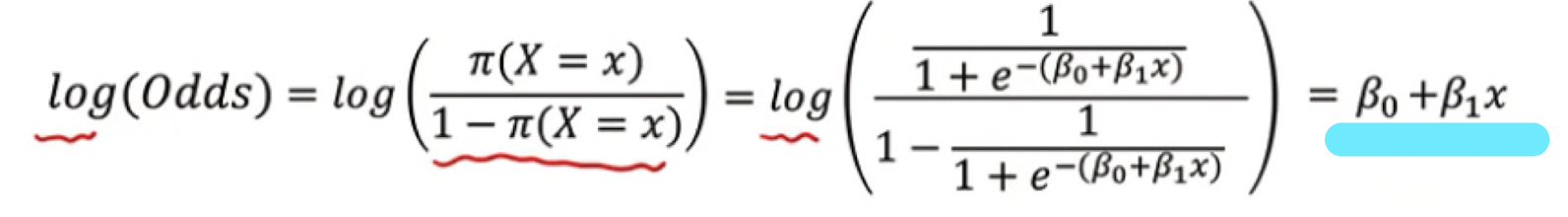
→ 놀랍게도 승산에 로그를 취한 형태는 다시 선형결합의 공식으로 돌아온다.
→ 위와 같은 변화를 우리는 로짓 변환 (logit transformation)이라 부른다.
→ 만약 입력 변수가 여러개인, 다중로지스틱 회귀라고 한다면?

따라서 위 과정을 통해 좌측의 exponential 이 섞인 식이 log(odd)로 취하면 선형 결합의 형태로 바뀐다.


오케이 이제 이 승산 개념을 머리에 박아두고,
β0 , β1 파라미터 추정을 진행해보겠다.
6. β0 , β1 파라미터 추정의 방법 : MLE (최대 우도 추정법)***
6.1 베르누이 확률 함수
2번에서 우리는 로지스틱 회귀가 베르누이 확률 분포를 따르는 것을 확인했다.


→ 여기서 확률 µ 를 P로, x를 yi로 바꿔서 표현하자면 이렇게 표현할 수 있다.

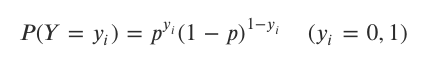
우리의 목표는 결국 입력 데이터(x1, x2, ... xn) 에 대해서
(타겟값이 0인 경우는) 결과값 Y가 0일 확률
(타겟값이 1인 경우는) 결과값 Y가 1일 확률을 최대화하는 파라미터 β0 , β1 를 찾는 것이다.
바로 MLE를 활용해서 !
MLE 최대 우도 추정법은 확률 모형의 모수를 추정할 때 일반적으로 사용되는 방법이다.
6.2. 우도 (=가능도, likelihood)
: 어떤 고정된 값이 특정 분포에서 나왔을 확률
이게 원래의 확률 개념과 헷갈릴 수 있는데, 예시를 통해서 설명하자면,
| 확률 | 가능도 | |
| 개념 | 어떤 고정된 분포에서 특정 값이 나올 확률 | 어떤 고정된 값이 특정 분포에서 왔을 확률 |
| 예시1. 불연속 사건 | 주사위 던지기에서 6이 나올 확률 | 주사위 던지기에서 6이 나왔는데 이건 어떤 분포에서 나왔는지 |
| 예시2. 연속사건 | A의 키가 164~165 일 확률 (확률 밀도 함수의 면적) |
A의 키가 164인데, 이 값은 어떤 분포에서 나왔는지에 대한 확률 (확률 밀도 함수의 y값) |
# 최대 우도? 확률에서 데이터를 가장 잘 설명할 수 있는 확률을 찾기
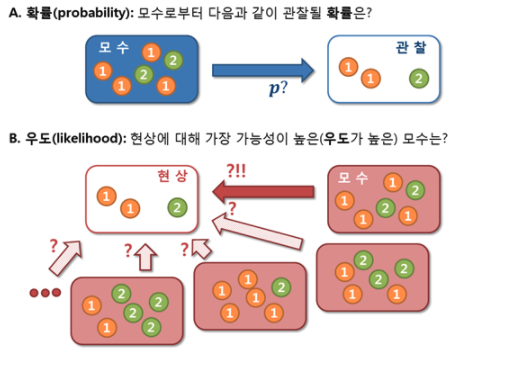
# 우도(가능도)를 계산하는 방법은?
가능도는 데이터가 주어졌을 때, 주어진 데이터가 해당 분포로부터 나왔을 가능성 말한다.
수치적으로 이 가능도를 계산하기 위해서는
각 데이터 샘플에서 후보 분포에 대한 높이(즉, likelihood 기여도)를 계산해서 다 곱한 것
6.3. MLE로 파라미터 추정***
1) 베르누이 확률 함수 :

베르누이 확률 함수에서 x를 y로 바꿔서 표현하자면,

2) 가능도 함수 : y로 바꾼 확률 함수 여러번 곱하기
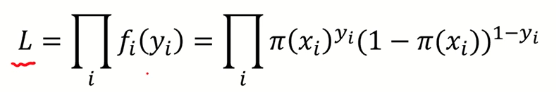
3) 앞에 log를 취해서 log-likelihood 계산

+) 5번 승산의 개념 여기서 등장 !!! log(odd)는 아래와 같은 선형결합으로 전개된다.
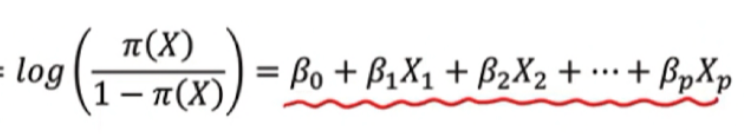
4) log likelihood 함수를 최대화 하는 파라미터를 찾는 것이 목적
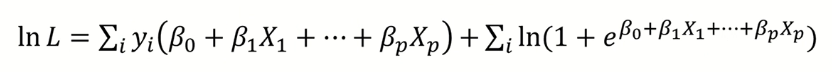
하지만, 베타에 대해 비선형 함수 이므로 명시적인 해를 찾기 어려움
수치 최적화 알고리즘을 활용해서 해를 구함
log likelihood를 최대화 시킨다 == cross entropy를 최소화 시킨다.
5) cross entropy : log likelihood 기댓값에 (-) 붙인 개념

+) 어떤 데이터가 0 또는 1로 predict될 확률은 ŷ , 1−ŷ 이므로 그 데이터의 likelihood 식은

y=1 일 때 y^를 최대화시켜야 하고, y=0일 때는 (1−ŷ )를 최대화시키는게 likelihood의 목적, 여기에 log를 씌우면
| log likelihood 최대화 | cross entropy |
 |
 |
따라서 log likelihood 함수를 최대화 시키는 것이 cross entropy를 최소화 시키는 것
6번의 결론, cross entropy 값을 최소화 하는 파라미터 β0 , β1 찾자 !!!!!
7. 결과 및 해석

7.1. 승산 비율 :

7.2. 예시 사례 - 신용카드 대출
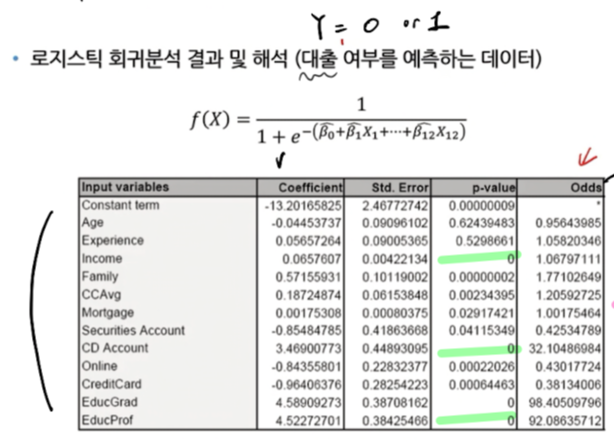
1) coefficient : 추정된 파라미터의 값
해당 변수가 1단위 증가할 때마다 log odd 의 변화량
양수이면 성공확률과 양의 상관관계, 음수면 성공확률과 음의 상관관계
(ex.credit card와 대출은 음의 상관관계, 수입과 대출은 양의 상관관계)
2) std.Error : 구간 추정을 할 때 필요한 개념,
3) p-value :
해당 변수가 통계적으로 유의미한지, Y와 관계가 있는지
"베타 값이 0" : 귀무가설
pvalue 가 작으면 귀무가설 기각 (해당 파라미터 Y와 관계 있음, 중요하다)
pvalue 가 크면 귀무가설 통과 (해당 파라미터 Y와 관계 없음, 중요하지 않다)
4) odds (odds ratio) ****
나머지 입력 변수는 모두 고정시킨 상태에서 한 변수를 1단위 증가 시켰을 때 변화하는 odd의 비율
Experience 1.058 : 경험이 1년 더 많으면 대출 확률이 1.058배 증가
Creditcard 0.38 : 신용카드가 1개더 있으면 대출 확률이 0.38배 감소
7.3. 예시 사례 - 질병 유무 확인

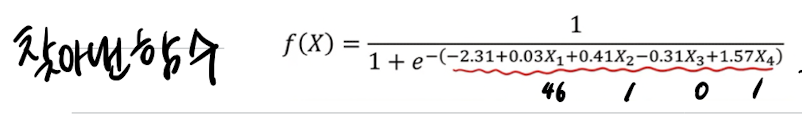

참고 link :
2)
https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
3)
https://angeloyeo.github.io/2020/07/17/MLE.html



댓글