0. 문제 정의
" Time series regression but ... Quantile regression ! "
input(test 하나의 csv) : 0 ~ 6 일치 데이터 입력 (30분 단위 시계열 데이터)
24시간 *2개 * 7일 = 336 row
output : 7,8일치 30분 단위 타겟값 예측 (regression)
24시간 * 2개 * 2일 = 96 row
하지만 이때 예측에서 반환되는 것은 Quantile 값이어야함.
즉, 30분 간격의 예측값에 대한 10%,20%,...90% 총 아홉개의 quantile
1. Quantile regression (분위 회귀) ?
참고 자료 :
0) Quantile ?
Quantile 은 확률 분포를 동등한 확률 구간으로 나누는 구분 눈금들 (Cut-Points) 또는 어떤 관찰된 샘플 데이터를 동등한 범위들도 잘라내는 구분자
# IQR (InterQuartile Range, 사분범위)
일반적으로 사용되는 사분범위는 0.25 확률 구간으로 나눈 것 또는
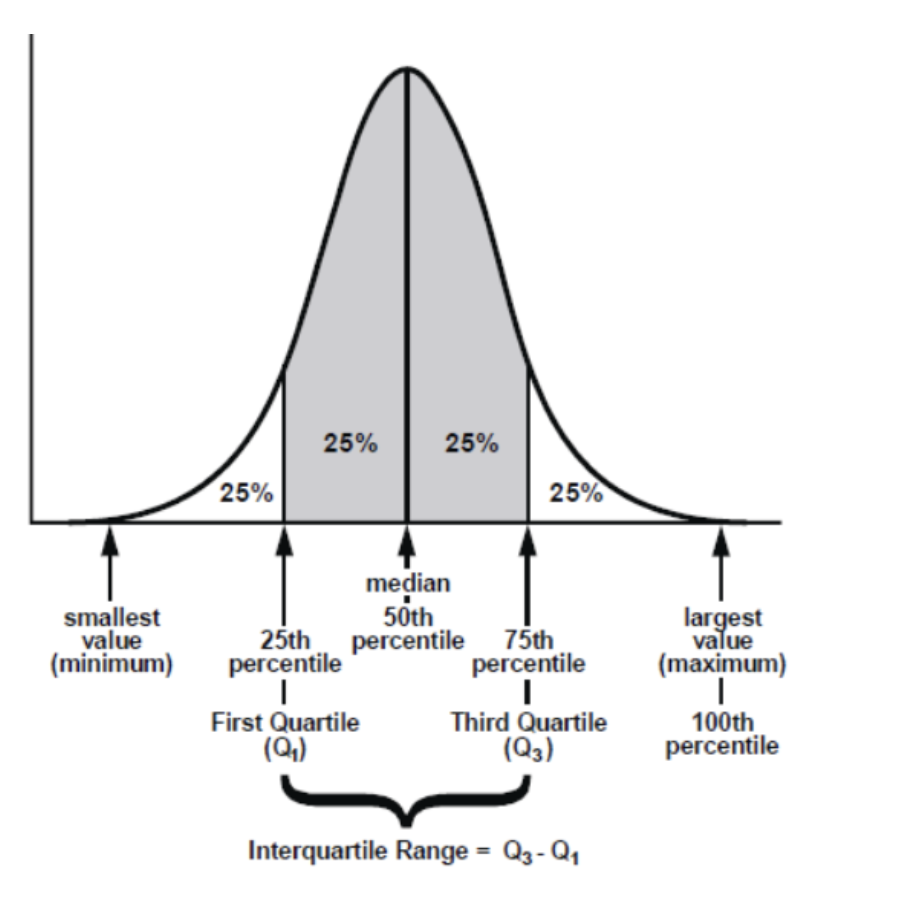
예를 들어보면, 사분위수 (Quartile) 를 많이 사용하는데,
4-Quantile 이라고 생각하면 샘플 데이터를 4개의 동등한 구간으로 잘라내기 위한 구분자는 3개가 된다. Q1, Q2, Q3 와 같이 표현한다.
1) Quantile regression
만약 IQR 로 Quantile regression 을 만든다면 --> 각 Quantile 0.25, 0.5, 0.75 1 총 4개의 모델로 구성됨
각각의 모델은 Quantile 값을 기준으로 loss에 가중치를 부여함 ==> 이를 pinball loss 라 부름
2) pinball loss
일반적으로 사용되는 회귀에서는 MSE(=OLS) 최소 제곱법, MAE 평균 절대 오차가 loss 값이 되지만
해당 모델에서는 pinball loss 가 사용됨
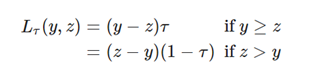
| *** 공식 뜯어보면 *** 실제값 : y / 예측값 : z / Quantile 값 y(정답)이 10인데, z(예측값이) 7인 경우 Quantile 0.1 모델에서 loss 는 (10-7) * 0.1 = 0.3 Quantile 0.9 모델에서 loss 는 (10-7) * 0.9 = 2.7 ==> overforecast 유도 Quantile 이 큰 값의 모델에서 loss 가 커짐 -> 값이 작아지도록 유도 2) 예측값이 정답보다 큰 경우 (z>y) y(정답)이 10인데, z(예측값이) 12인 경우 Quantile 0.1 모델에서 loss 는 (12-10)(1-0.1) = 2 * 0.9 = 1.8 ==> underforecast 유도 Quantile 0.9 모델에서 loss 는 (12-10)(1-0.9) = 2* 0.1 = 0.2 Quantile 이 작은 값의 모델에서 loss 가 커짐 -> 값이 커지도록 유도
3) 정답을 넣었을 경우 : 모든 Quantile 모델에서 loss 값이 0 이 나옴 (회귀 분석과 같은 원리) |
- 높은 quantile 값에서는 측정된 값이 예측값보다 낮아야 함 >> overforecast 유도
- 반대로 낮은 quantile값에서는 측정된 값이 예측값보다 높아야 함 >> underforecast 유도
- 최종 목표는 각 분위수 모델에서 0 이 나오는 것 !
+) OLS (Ordinary Least Squares) 의 문제점을 보완
OLS 최소 자승법 (= LSM (Least Square Method) 최소 제곱법)
우리가 일반적으로 알고 있는 회귀의 결과 값
선형 회귀 라면 ^y = wx+b / 오차는 = 차의 제곱의 평균 !
-- 하지만 여기에는 3가지 전제가 있었음
a. 독립변수 Xi 는 랜덤하지 않은 고정된 수
b.
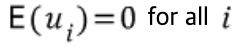
c. --> 동분산이어야 한다는 제약조건

==> 따라서 타겟값이 동분산이 아닌 경우에는 (이분산인 경우에는) QR regression 을 사용해야한다.
homoscedasticity(동분산) VS heteroscedasticity (이분산)
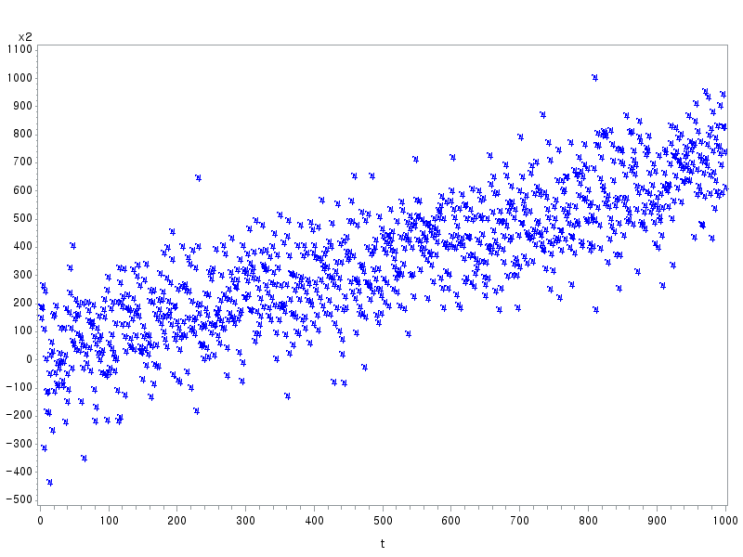
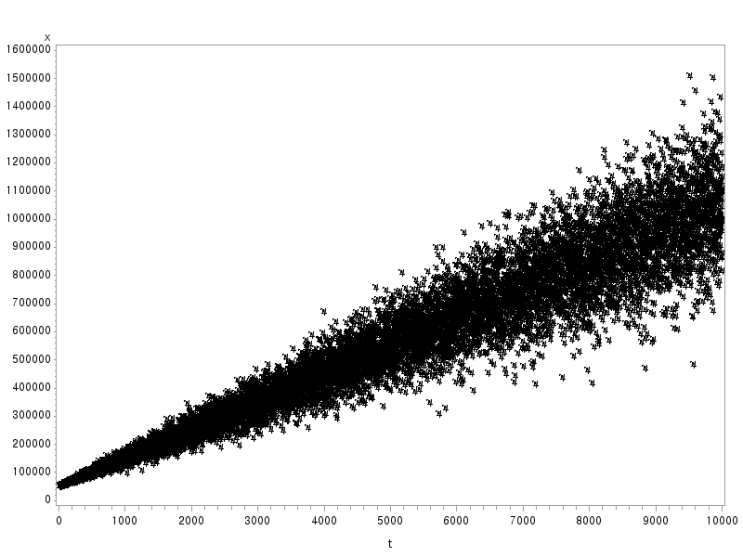
분위회귀분석은 종속변수의 특정한 조건부 분위를 중심으로 독립변수(x)와 종속변수(y-target)의 관계를 분석
독립변수와 종속변수의 기대값 간의 선형관계 만을 분석하는 최소자승법(OLS)에 비해
더욱 다양한 측면에서 두 변수간의 전반적인 관계를 분석
ex. 나이대 별 BMI 지수를 예측하는 문제
: 수치의 IQR 분위수가 중요한 경우 *** (35 이상 비만, 12 이하 영양실조 )
40대 남성 2명 있고 각각 BMI 37,10
37+10 = 47/2 = 23.5 정상 이라고 판단할 수 있는가? 평균으로 뚝딱 계산해버리면 안되는 문제들
3) 공식 뜯어 보기
BOK%20%EA%B2%BD%EC%A0%9C%EB%A6%AC%EB%B7%B0%20No.2014-5.pdf 페이지 20
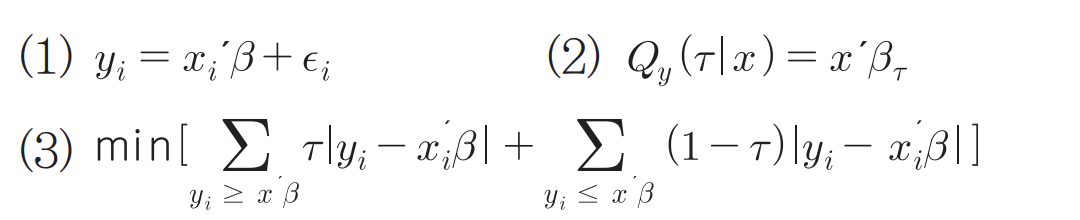
τ: 퀀타일 값 (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9)
y: 실제 값
(1) 일반적인 회귀 공식
(2) 입력된 xi 에 대해 y의 τ-조건부 분위수함수(conditional quantile function)
τ(타우) 가 0.5 라면 0.5 조건부 분위수 함수 값
(3) 2번의 분위회귀추정치 β⌒τ는 (3)번의 최소화 문제를 만족하는 해로부터 구할 수 있음
(3) Lτ: pinball loss 함수 --> 3번 공식 조금더 살펴보기 : y 가 타겟값, z 가 예측값
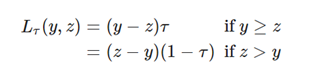
==> 정리
분위회귀는 각 n개의 분위수에 따른 n개의 분위 회귀 모델이 만드는 방식
이때 각각의 분위회귀 모델은 pinball loss 통해 타겟값에 가까운 예측값을 회귀
총 만들어진 n개의 모델에서 나온 값을 통해, 우리는 n개 후보의 예측값, 즉 예측값의 범위를 추론해 낼 수 있는 것임
2. 코드 예제들 !!
dataman-git/codes_for_articles
Contribute to dataman-git/codes_for_articles development by creating an account on GitHub.
github.com
[Stats] 등분산 vs. 이분산 설명
/******************************************************************************************************************* -- Title : [Stats] 등분산 vs. 이분산 설명 -- Reference : elearning.kocw.net/cont..
dbrang.tistory.com




댓글