1. 문제 설명
1018번: 체스판 다시 칠하기
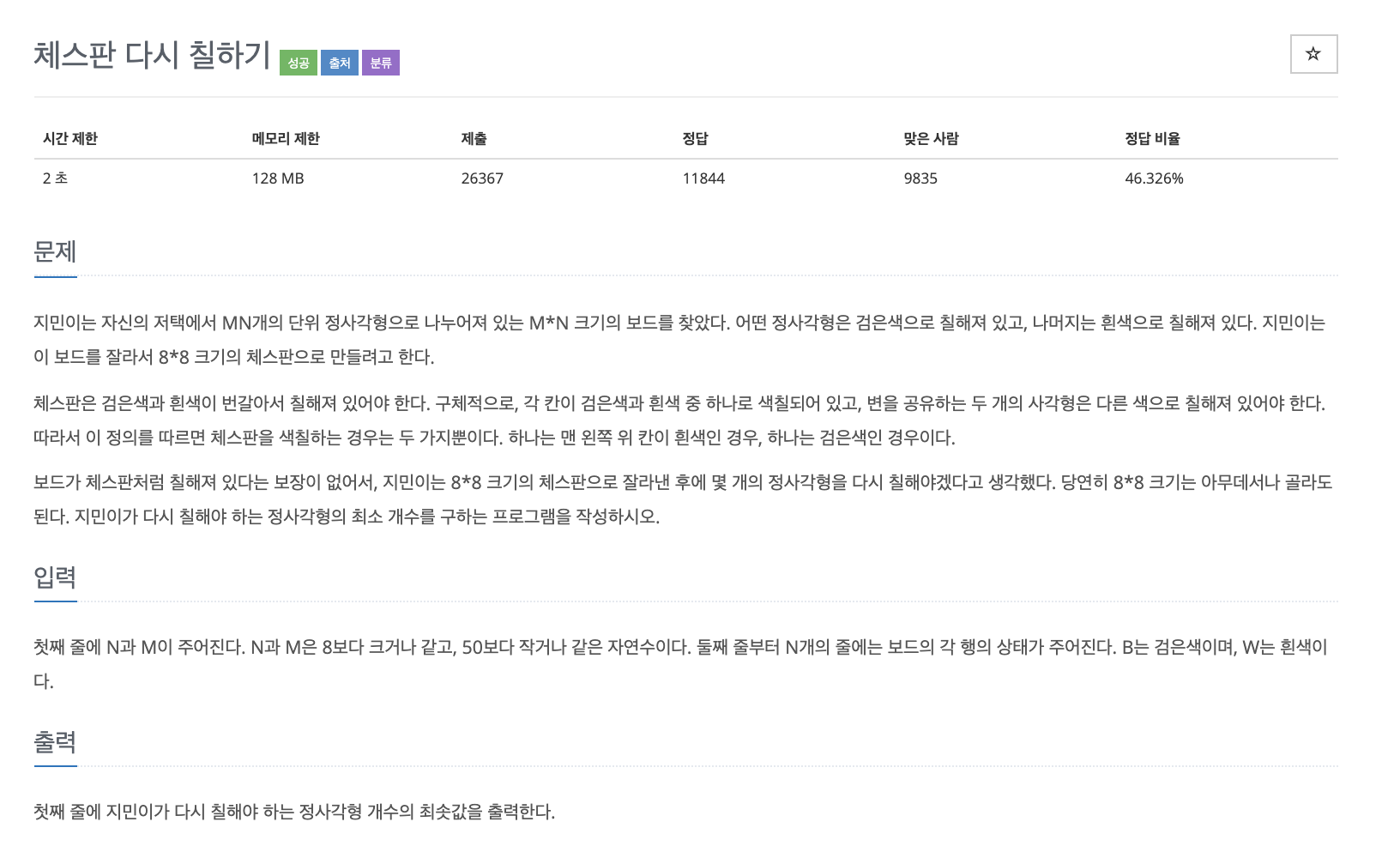
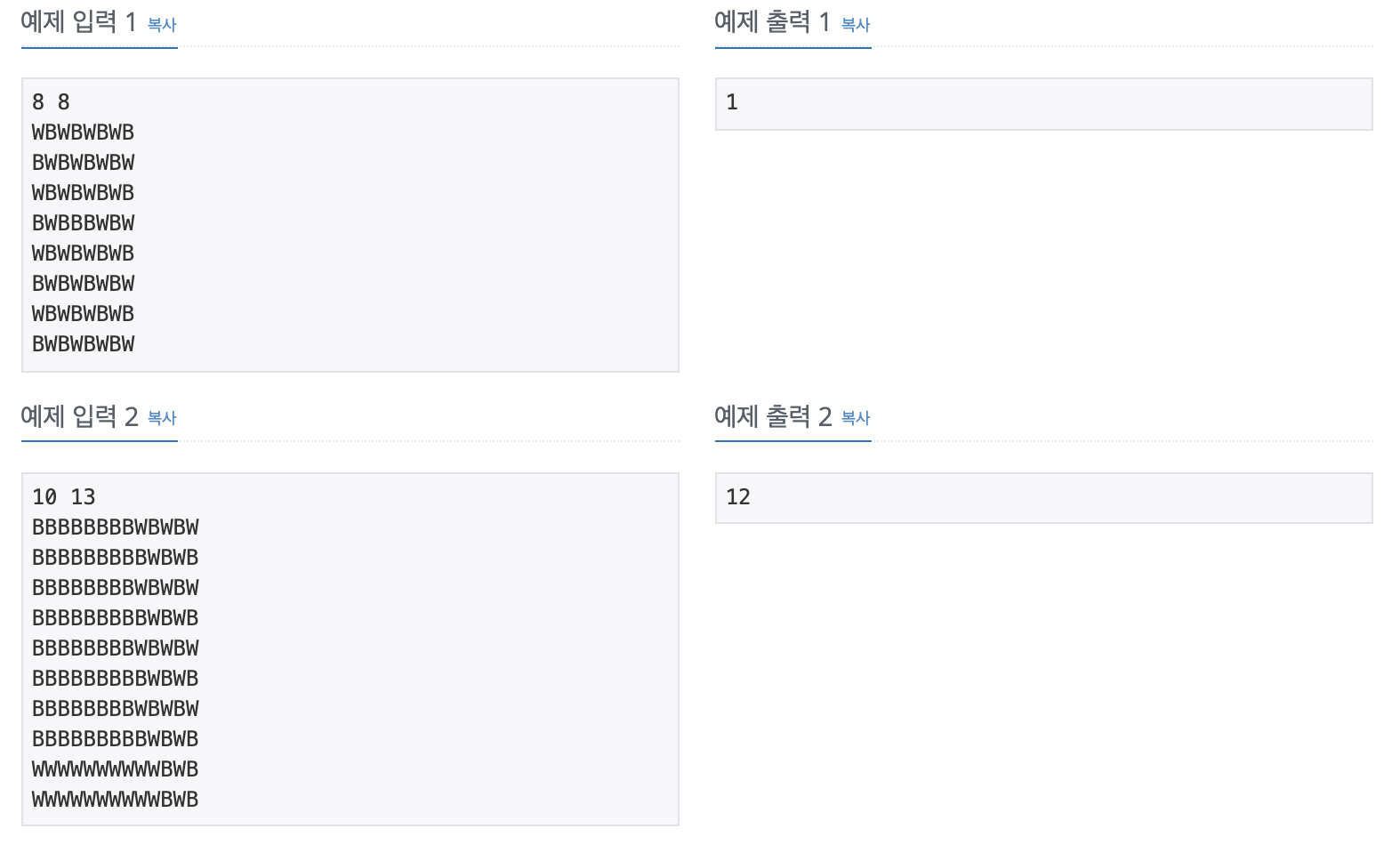
첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
www.acmicpc.net
2. 풀이
0. 탐색방법은 윈도우를 옮기며
CNN 윈도우 사이즈 만큼 탐색하듯이 해줘야 한다.
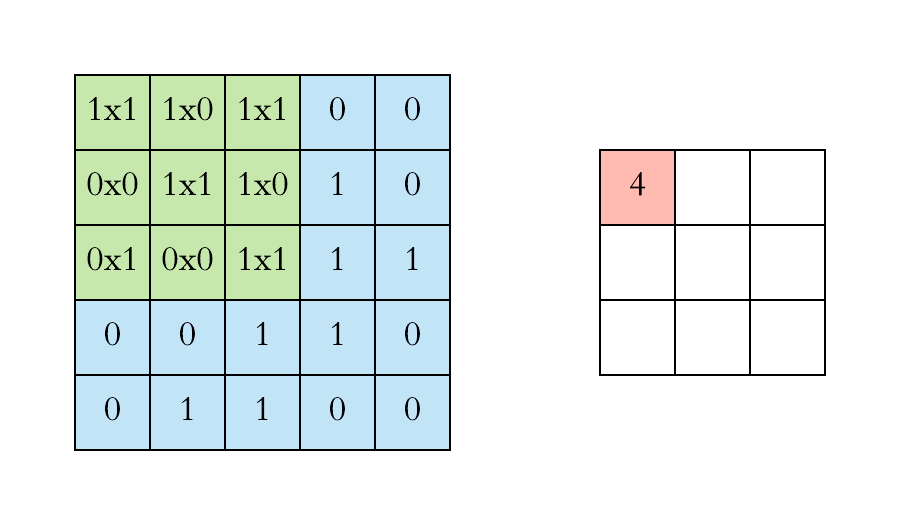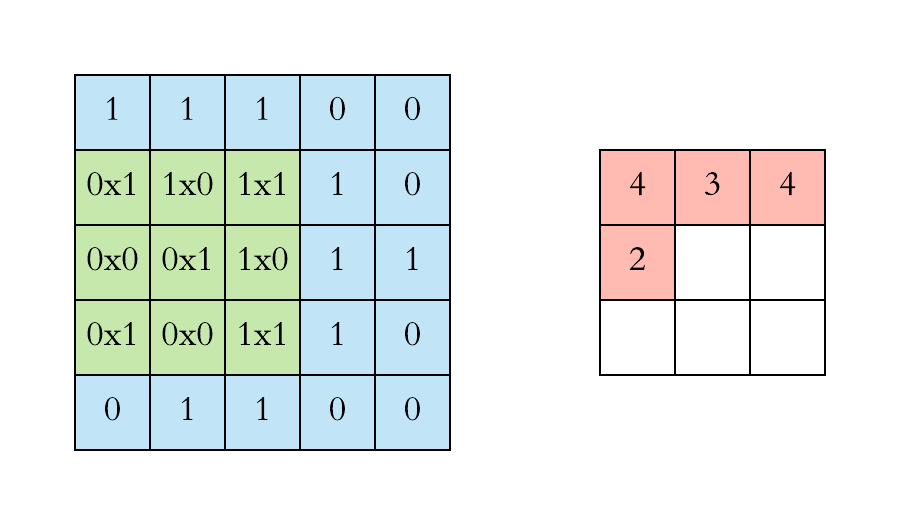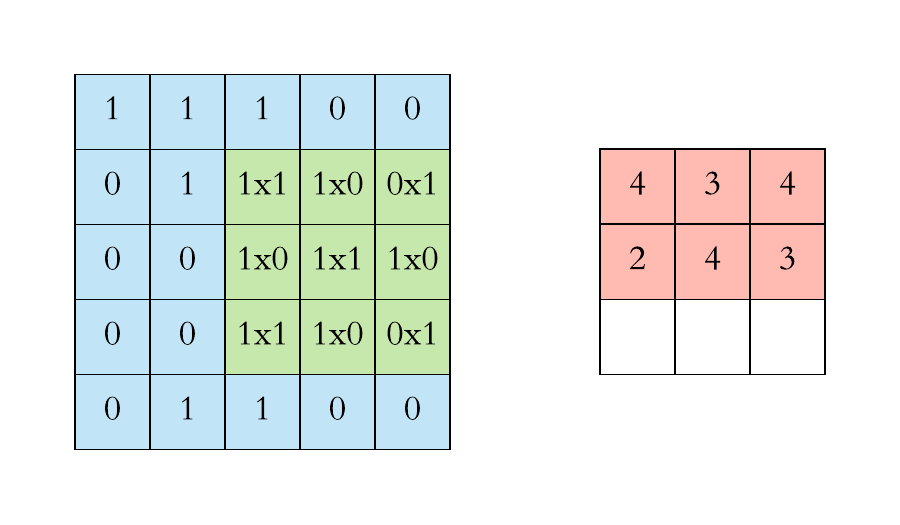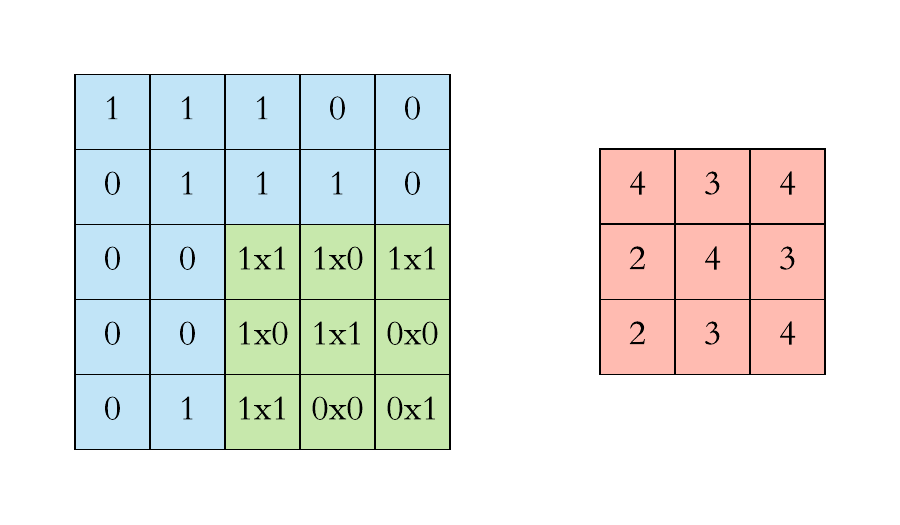
여기서 초록색이 움직이는 것 처럼 !!! (빨간색은 무시하세요... CNN 알고리즘에서 긁어온거라..!)
즉 가세로가 8 초과인 경우는 행과 열을 움직여가며
8*8 사이즈 매트릭스 중 규칙에 어긋난 갯수를 구해야한다.
그중 가장 적게 어긋난 갯수를 반환해주는게 문제의 정답 !
1. WB를 어떻게 잡아낼까.
처음 WB 를 어떻게 찾아낼지 고민을 많이했다. 그리디 문제로 접근해서
처음 "WB" 가 입력되는 갯수를 새어서 가장 많이 등장하는 범위를 구하려 했으나.
문제점 1) 행의 경우는 간단하지만, 열을 하려면 다시 매트릭스를 해체하여 O(N^2) 만큼의 시간복잡도가 소요된다.
문제점 2) 또 문제의 핵심은 수정해야하는 갯수를 구하는거니까 문제의 방향과도 맞지 않다고 생각했다.
==> 결국 각 요소들을 일일이 살펴보는 수 밖에 없음 이때 핵심은 시작 키에 따라서 정답이 두가지로 나뉜다는 거다 !!
 |
 |
좌측의 경우처럼
8*8 매트릭스의 시작을 W 로 한다면 (0인덱스를 기준으로 하여)
행 인덱스 짝수 and 열 인덱스 짝수 면 ==> B
행 인덱스 홀수 and 열 인덱스 홀수 면 ==> B
행 인덱스 홀수 and 열 인덱스 짝수 면 ==> W
행 인덱스 짝수 and 열 인덱스 짝수 면 ==> W
반대로 우측의 경우처럼
8*8 매트릭스의 시작을 B 로 한다면 (0인덱스를 기준으로 하여)
행 인덱스 짝수 and 열 인덱스 짝수 면 ==> W
행 인덱스 홀수 and 열 인덱스 홀수 면 ==> W
행 인덱스 홀수 and 열 인덱스 짝수 면 ==> B
행 인덱스 짝수 and 열 인덱스 짝수 면 ==> B
이 두가지 경우를 모두 고려해야하여 매칭이 되지 않는 갯수 (수정해야할 갯수)를 각각 구하고
둘 중 더 작은 값을 반환해준다.
이 과정을 M과 N에서 생성되는 8*8 매트릭스 갯수만큼 반복한뒤
최종적으로 가장 작은 값을 반환해주면, 끝
import sys
def check_BW(matrix):
case1_not_match = 0
case2_not_match = 0
# case 1 시작점(0,0)이 W 인경우
for x in range(8):
for y in range(8):
if ((x % 2 == 0) and (y % 2 == 0)) or ((x % 2 == 1) and (y % 2 == 1)): # 행짝 열짝, 행홀 열홀
if matrix[x][y] != "W":
case1_not_match += 1
elif ((x % 2 == 1) and (y % 2 == 0) or (x % 2 == 0) and (y % 2 == 1)): # 행홀 열짝, 행짝 열홀
if matrix[x][y] != "B":
case1_not_match += 1
# case 2 시작점(0,0)이 B 인경우
for x in range(8):
for y in range(8):
if ((x % 2 == 0) and (y % 2 == 0)) or ((x % 2 == 1) and (y % 2 == 1)): # 행짝 열짝, 행홀 열홀
if matrix[x][y] != "B":
case2_not_match += 1
elif ((x % 2 == 1) and (y % 2 == 0) or (x % 2 == 0) and (y % 2 == 1)): # 행홀 열짝, 행짝 열홀
if matrix[x][y] != "W":
case2_not_match += 1
return min(case1_not_match, case2_not_match)
def solution():
input_list = []
M, N = map(int, sys.stdin.readline().split())
for idx in range(M):
input_list.append([i for i in sys.stdin.readline()][:-1])
min_revise_cnt = 123041234723842
for row in range(M-7):
for col in range(N-7):
# 8*8 매트릭스로 자르기
slice_mat = [one_row[col:col+8] for one_row in input_list[row:row+8]]
revise_cnt = check_BW(slice_mat)
min_revise_cnt = min(min_revise_cnt, revise_cnt)
return min_revise_cnt
print(solution())
1. solution
solution에서 입력을 받은 후, 입력된 매트릭스를 8*8 로 잘라서 확인하도록 이중 for 문을 돌린다.
2. check_BW
앞서 설명했듯 시작을 B W 두가지 경우로 나누어 매칭을 시켜보고
매칭이 안되는 경우 case not match1 case not match2 변수에 각각 담기게 했다.
그리고 그중 더 작은 값을 리턴하며 check_BW가 끝난다.
다시 1. solution
check_BW에서 값이 반환될때마다, 이전 값보다 작으면 업데이트 시켜주는 방식으로 코드를 짰다.
임의로 맨처음 min에 큰 값을 넣어두었고, 모든 범위를 다 돌면 가장 작은 값이 저 안에 담기게 된다.
결과 값을 다 담아두고 마지막에 min을 뽑는거보다 저게 더 시간복잡도가 덜 걸려서 저 방법을 선호한다.
참고 링크 :
[백준] 1018번 : 체스판 다시 칠하기 in python 파이썬
파이썬으로 백준풀기 :: 1018 체스판 다시 칠하기 https://www.acmicpc.net/problem/1018 코드 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def check_BW(ex): ..
leedakyeong.tistory.com
3. 정리
왜 스스로 저 인덱스 해결 방법이 생각나지 않을까.
완전 탐색말고 더 괜찮은 방법이 있을꺼라 집착해서 그럴수도...!
매트릭스 매칭 문제는 인덱스 홀짝으로 쉽게 풀수 있다는 것을 기억하면서 비슷한 문제에서도 이 풀이법 적용해보기 !
'Study > Algorithm & Data structure' 카테고리의 다른 글
| [프로그래머스][탐색] 스킬트리(201013) (0) | 2020.10.14 |
|---|---|
| [백준] 1026번 보물 python (201011) (0) | 2020.10.11 |
| [프로그래머스][DFS] 여행경로(201008) (0) | 2020.10.08 |
| [프로그래머스][DFS] 여행경로(201008) (0) | 2020.10.08 |
| [프로그래머스][DFS] N-queen (201008) (0) | 2020.10.08 |



댓글