백준과 프로그래머스 공통으로 있는 문제이며 전형적인 백트레킹 DFS 문제이다.
[ 백트래킹 DFS 문제는 뭔가 ? ]
[알고리즘] 되추적(Backtracking)을 알아보자.
오늘의 주제는 되추적(Backtracking) 이다. 저번 포스팅인 깊이우선탐색(Depth-First Search)과 넓이우선탐색(Breath-First Search)의 몸풀기를 거치고 최단경로(Shortest Path) 알고리즘에 들어가는 첫 걸음이라..
idea-sketch.tistory.com
[ 프로그래머스 풀이 ]
1. 문제 설명
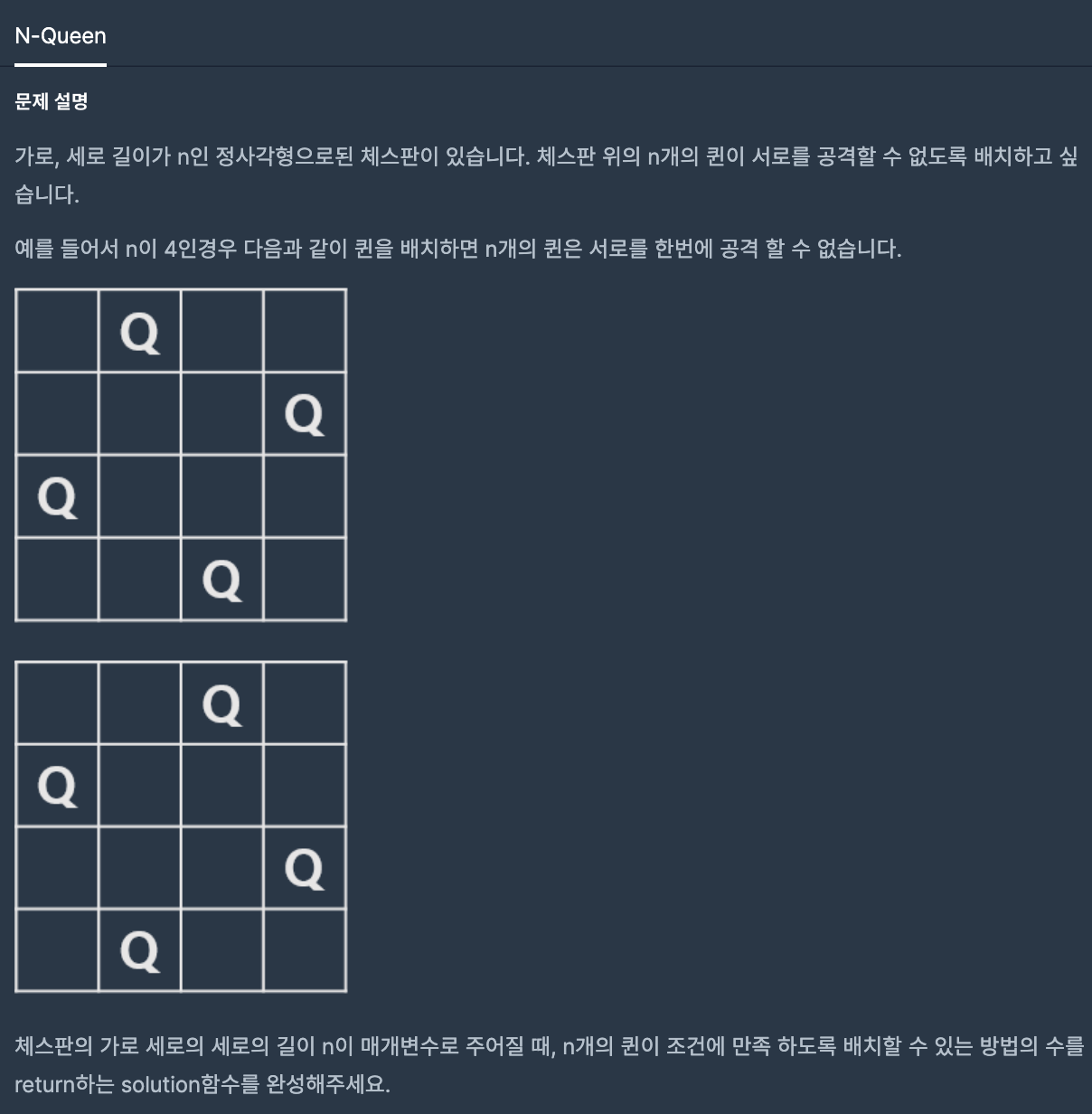

핵심
* [퀸 조건] 같은 행 렬에 대각선에 위치해서는 안된다.
* 첫 행부터 각 행마다 조건에 맞게 설치해보고 마지막 행까지 설치하기 전에 n 개가 설치되면, 한 개의 맵 완성
+) 대각선 계산 방법은 은근 쉽다.
왼 -> 오 대각선은 각 (x,y)의 차가 같고 ex. (1,1) (2,2) (3,3) (4,4) (5,5)
오 -> 왼 대각선은 각 (x,y)의 합이 같다. ex. (1,5) (2,4) (3,3) (4,2) (5,1)
2. 풀이
정답 코드는 아래와 같으나 설명이 없다면 이해하기가 몹시 어렵다.
def solution(n):
# 1. 퀸 세울수 있 방문 좌표 저장
columns = set()
diagonals1 = set()
diagonals2 = set()
return dfs(n, 0, columns, diagonals1, diagonals2)
def dfs(n, row, columns, diagonals1, diagonals2):
# 2. 재귀함수가 멈추는 조건 - 모든 row에 다가 말을 하나씩 다 놨을때 1개의 맵 완성되었다고 반환하도록.
if row == n:
return 1
# 3. 입력된 로우를 기준으로 칼럼별 탐색
### check point
cnt = 0
for col in range(n):
# 4 배치 가능 여부 확인
if col in columns or (row + col) in diagonals1 or (row - col) in diagonals2:
continue # -> 불가능이면 바로 다음 컬럼
# 5 퀸 배치시키고 좌표 저장
columns.add(col)
diagonals1.add(row + col)
diagonals2.add(row - col)
# 6 해당 방문 좌표에서 밑에 줄 퀸 설치 가능 확인 --> dfs 다시 탐색
cnt += dfs(n, row + 1, columns, diagonals1, diagonals2)
# 7 마지막 까지 돌았는데, (2번) n개 설치 다 못하면 , (5번) 배치시킨 퀸 철회
columns.remove(col)
diagonals1.remove(row + col)
diagonals2.remove(row - col)
return cnt
이렇게 총 7 단계로 나눠져 있는데,
1. solution 함수로 퀸 방문 좌표를 저장해두기
--> 대체로 재귀함수를 쓸때는 이렇게 저장 셋을 밖으로 빼둬야한다. (셋인 이유는 순서 상관없이 중복되는 값이 없는 좌표이기 때문에)
2. DFS 함수 멈추는 조건 설정 해두기
단순히 row == n 만 한 이유는
한 행(row)에 반드시 설치 되어야만, 그 다음 행 숫자로 넘어가기 때문에
row 가 2 라는 것은 여태 설치된 퀸이 2개라는 거고 설치된 퀸값과 목표값(n) 이 같아지면 원하는 맵 하나가 완성되기 때문에 1을 반환함
그리고 반환된 값은 6번에서 보듯이 cnt에 축적되고 마지막에 총 맵의 개수가 리턴되는 형식
3. 입력된 row를 기준으로 column 탐색
맨처음은 (0,0) -> (0,1) 이런식으로 칼럼을 늘려가며
4. 해당 지점에 배치 가능 여부를 확인함 --> 이전 설치된 것과 행/렬/대각선 겹치는지 셋으로 확인
설치 안된다면 다음 칼럼으로 (0,1)
5. 설치 가능하면 : 퀸 배치 시키고 좌표 저장
6. 다음 칼럼으로 넘어가지 않고 !!!!!! /
해당 지점을 기준으로 바로 밑에 퀸 설치 가능한지 확인 ->DFS 다시
** 여기서 계속계속 타고 들어가는 개념인거다..!
7. 마지막 까지 돌았으나, n개를 다 설치하지 못한다면 (2번조건)
설치한 퀸들을 철회해준다. (5번조건)
이것은 재귀 함수들을 빠져나오면서 실행되도록 재귀함수 밑에 적어줌
사실 재귀는 이렇게 말로 설명해서도 정말 이해가 안되어서 지독하게 일일이 다 찍어보았따.
**** 0 행 설치 시도 - 현재 CNT 0
배치 가능 0 0
-> 다음 행의 퀸배치 CNT 0 ( row 1 )
**** 1 행 설치 시도 - 현재 CNT 0
배치 불가 PASS ( 1 0 )
배치 불가 PASS ( 1 1 )
배치 가능 1 2
-> 다음 행의 퀸배치 CNT 0 ( row 2 )
**** 2 행 설치 시도 - 현재 CNT 0
배치 불가 PASS ( 2 0 )
배치 불가 PASS ( 2 1 )
배치 불가 PASS ( 2 2 )
배치 불가 PASS ( 2 3 )
--- :(( 4개 배치 실패
Remove 1 2 --> 이전 설치 지점 삭제하는 거 (7번코드)
-- 다시1에서 배치 가능 지점 찾기
배치 가능 1 3 --> 열을 늘리는 for 문으로 다음 배치 가능 지점으로 다시 재귀시도 (3번 포문 -> 45 다시 진행)
-> 다음 행의 퀸배치 CNT 0 ( row 2 )
**** 2 행 설치 시도 - 현재 CNT 0
배치 불가 PASS ( 2 0 )
배치 가능 2 1
-> 다음 행의 퀸배치 CNT 0 ( row 3 )
**** 3 행 설치 시도 - 현재 CNT 0
배치 불가 PASS ( 3 0 )
배치 불가 PASS ( 3 1 )
배치 불가 PASS ( 3 2 )
배치 불가 PASS ( 3 3 )
--- :(( 4개 배치 실패
.... 너무 길어서 하략
대강 이런식이다. (출력 코드는 아래와 같음)
def solution(n):
# 1. 퀸 세울수 있 방문 좌표 저장
columns = set()
diagonals1 = set()
diagonals2 = set()
return dfs(n, 0, columns, diagonals1, diagonals2)
def dfs(n, row, columns, diagonals1, diagonals2):
# 2. 재귀함수가 멈추는 조건 - 모든 row에 다가 말을 하나씩 다 놨을때
if row == n:
print(f"\n ================ {n}개 배치 완성!!")
return 1
# 3. 입력된 로우를 기준으로 칼럼별 탐색
### check point
cnt = 0
print("**** ",row,"행 설치 시도 - 현재 CNT",cnt)
for col in range(n):
# 4 배치 가능 여부 확인
if col in columns or (row + col) in diagonals1 or (row - col) in diagonals2:
print("\t 배치 불가 PASS","(",row, col,")")
continue # 4.1 불가능이면 바로 다음 컬럼
# 4.2 가능이면
# 1) 방문 좌표 저장
print("\t 배치 가능",row, col)
columns.add(col)
diagonals1.add(row + col)
diagonals2.add(row - col)
# 2) 해당 방문 좌표에서 밑에 줄 퀸 설치 가능 확인 --> 만약 다 된다면
print(" -> 다음 행의 퀸배치","CNT",cnt,"( row",row+1,")")
cnt += dfs(n, row + 1, columns, diagonals1, diagonals2)
# 3) 원하는 개수만큼 설치 실패하면 저장공간에서 삭제
print(f"--- :(( {n}개 배치 실패 ")
print("Remove", row, col)
print(f"--- 다시{row}에서 배치 가능 지점 찾기")
columns.remove(col)
diagonals1.remove(row + col)
diagonals2.remove(row - col)
if col == n-1:
print("~~~~~~~ 탐색 끝 ~~~~~~~~~~~")
return cnt
3. 정리
더 많은 DFS를 풀어봐야 알겠지만, 저게 약간 국룰인거 같다.
DFS는 1) 탈출조건 설정 / 2) 타고타고 들어가기 / 3) 타고들어가다 막혔을때 앞에꺼 취소하는 코드
그리고 이 모든 걸 저장해둘 셋은 다른 함수에 만들어두고
일단 다른 문제도 풀어봐야겠다 !
'Study > Algorithm & Data structure' 카테고리의 다른 글
| [프로그래머스][DFS] 여행경로(201008) (0) | 2020.10.08 |
|---|---|
| [프로그래머스][DFS] 여행경로(201008) (0) | 2020.10.08 |
| [프로그래머스] [BinarySearch] 가로등 (201008) (0) | 2020.10.08 |
| [프로그래머스][queue/BFS] FloodFill (0) | 2020.10.08 |
| [프로그래머스][queue/BFS] 전염병 (0) | 2020.10.08 |




댓글