1. 문제 설명
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 �
www.acmicpc.net

2. 풀이
코드 풀이전에 오늘은 이 문제 유형의 개념을 살펴볼까 한다 !
이렇게 각 노드, 가중치를 주고 각 노드들을 다 이어주는 최소 가중치 경로를 찾는 문제를 최소 신장트리 MST 라 부른다.
그리고 여기에는 크루스칼, 프림 2가지 알고리즘 풀이 법이 있다.
www.fun-coding.org/Chapter20-kruskal-live.html
파이썬과 컴퓨터 사이언스(고급 알고리즘): 최소 신장 트리 (Kruskal Algorithm) - 잔재미코딩
4. 크루스칼 알고리즘 (Kruskal's algorithm)¶ 모든 정점을 독립적인 집합으로 만든다. 모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다. 두 정점의 최상위 ��
www.fun-coding.org
1) 크루스칼 ( + 유니온 랭크)
: 크루스칼의 핵심은 비용이 작은걸 먼저 연결시켜주는데 사이클 여부를 확인 하면서 연결시켜 주는 것
+) 사이클은 부모가 같아서 계속 트리가 뻗어나가는게 아니라 거기 안에서 돌고 돌아버리는 현상을 말하는것
아래의 사진에 B - C - E 가 사이클의 예시임
따라서 해당 지점에서 연결된 최상위 부모를 확인하는게 ! 크루스칼의 특징
[ 순 서 ]

a. 모든 간선을 비용 기준으로 정렬한다 (비용이 가장 작은 간선이 가장 먼저 체크되도록 ! )***
b. 정렬된 간선을 차례로 꺼낸다
c. 이때 해당 간선의 최상위 정점 (연결된 부모)을 확인
d. 만약 그 두 부모가 같다면 이건 사이클이 되어버린다. --> 연결 x
(아래의 예시 3번 경우 B,C 의 관계가 그렇다.
만약 B C 를 연결시켜버리면, 해당 경로는 다른 경로로 뻗어나가지 않고 저 안에서 사이클이 형성되어버린다.
부모가 다르면 연결시켜줌 --> 연결 o
e. 이 때 연결을 시켜줄 때 누가 부모로 될지 정해야하는데, 그것은 rank 기준으로 한다.
만약 입력된 A, D 지점중 D의 랭크가 더 높다면, D를 부모로 해준다 (반대면 A가 부모가 된다)
만약 입력된 A,D 지점 모두 같은 랭크면 둘 중 하나 부모로 고르고 부모인 노드 랭크 높여주기
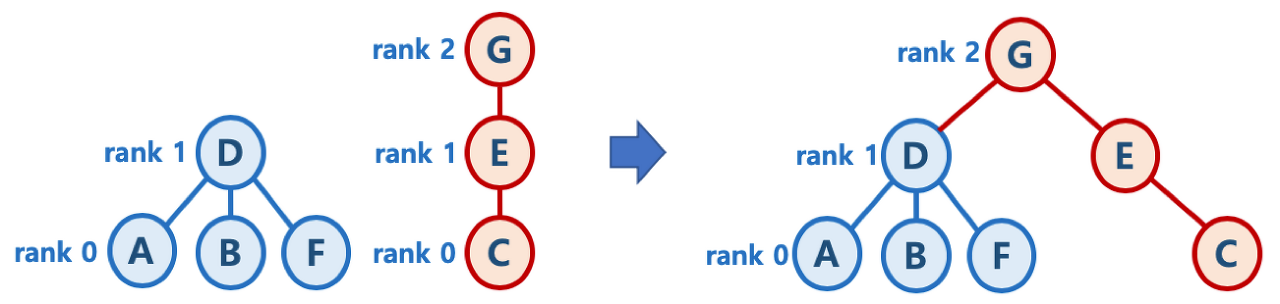
--> 예를 들어 좌측과 같이 랭크와 연결이 체크된 상황에서 D - G 의 간선을 그어야 한다면
D - G 의 랭크를 파악하고, 랭크가 더 큰 G를 부모로 매칭 시켜주는 개념이다.
이 5가지 단계를 코드로 구현하자면.. !
import sys
def find(node): # 해당 node 최상위 정점을 찾는다
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
def union(node1, node2): # 두 정점을 연결한다
# 사이클을 피하기 위해 최상위 부모 탐색
root1 = find(node1)
root2 = find(node2)
# 최상위 부모가 다르면 연결 가능
if root1 != root2:
# 랭크를 기준으로 부모 자식 결정 - 랭크 높이가 더 큰 노드가 부모
if rank[root1] > rank[root2]:
parent[root2] = root1
elif rank[root1] < rank[root2]:
parent[root1] = root2
else: # 둘의 랭크 높이가 같은 경우는 - default 로 root1 부모가 되게함.
parent[root2] = root1
rank[root1] += 1 # root2에 더하기 시켜줘
def kruskal(nodes, info_list):
# a. 모든 노드 간선 비용 기준으로 정렬
sor_info_list = sorted(info_list, key=lambda x: x[2])
# 부모관계, 랭크 정보 담기는 딕셔너리 초기화
for node in range(1,nodes+1):
parent[node] = node # 부모 정보가 담기게 됨 - 초기값은 자기자신
rank[node] = 0 # 트리 높이 정보 담기게 됨 - 초기 값은 1
total_aws = 0
# b. 간선 차례로 꺼내고 연결 시도
for one_info in sor_info_list:
node1, node2, weight = one_info
# c. 간선 최상위 부모 확인 - 같은지 아닌지
if find(node1) != find(node2):
union(node1, node2) # d. 같으면 연결 !
total_aws += weight # 연결 후 가중치 더해주기
return total_aws
if __name__ == "__main__":
nodes, line = map(int, sys.stdin.readline().split())
info_list = []
for _ in range(line):
info_list.append(list(map(int, sys.stdin.readline().split())))
parent = dict() # 각 노드들의 부모 정보
rank = dict() # 각 노드들의 랭크
kruskal(nodes, info_list)
중간에 부모를 찾고, 연결시켜주는 건 별도로 함수로 구현을 했다.
부모를 찾는게 재귀식으로 이루어져야하기 때문 !
다음 포스팅에서는 프림으로 풀어보겠음
'Study > Algorithm & Data structure' 카테고리의 다른 글
| [프로그래머스][greedy] 구명보트 (201019) (0) | 2020.10.19 |
|---|---|
| [백준] 킹(201017) (0) | 2020.10.17 |
| [프로그래머스][greedy] 섬연결하기(201015) (0) | 2020.10.15 |
| [프로그래머스][greedy] 단속카메라(201014) (0) | 2020.10.14 |
| [프로그래머스][탐색] 스킬트리(201013) (0) | 2020.10.14 |



댓글