1. Graph neural network란?
Image, Sequential data(=Sentence) 이외에 input data구조가 graph인 경우, 이 graph data를 학습해야할 때가 있다.
(ex. 영상에서의 graph, 분자구조 graph, Social graph ...)


Vertices / Node (=노드) : user, item, 원자
Edge (=엣지) : click, connectivity


+) spectral VS spatial
## Spatial
- 우리가 일반적으로 이해하고 있는 CNN 은 spatial
- Spatial graph convolution은 convolution 연산을 graph위에서 직접 수행하는 방식으로,
각 노드와 가깝게 연결된 이웃 노드들에 한해서 convolution 연산을 수행
- 즉, 노드와 이웃노드들을 특정 grid form으로 재배열하여 convolution 연산을 수행
- 그러나, 우리가 일반적으로 아는 CNN의 filter는 고정된 사이즈를 가집니다(그림 1.).

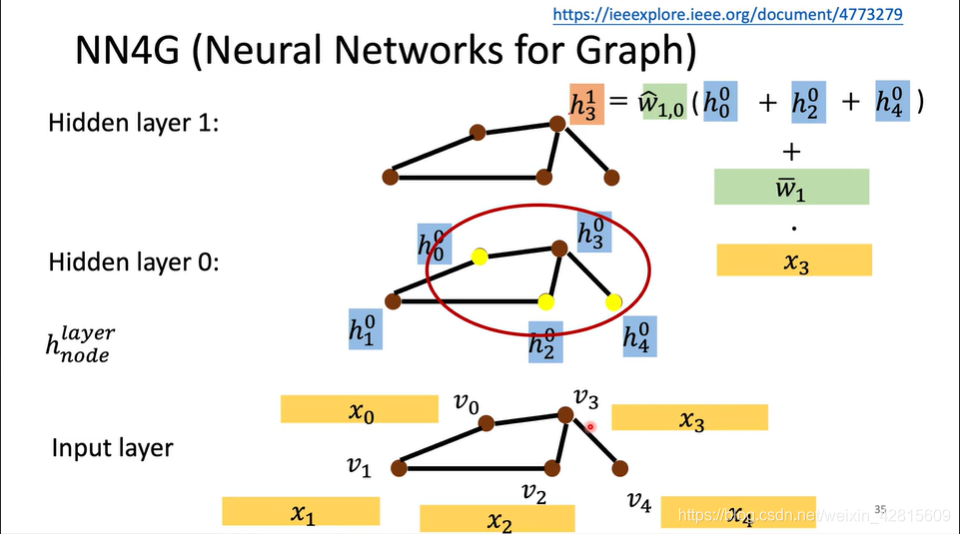
- spatial graph convolution 방식의 관건은 고정된 크기의 이웃 노드를 선택하는 것
- Spatial graph convolution의 또다른 관건은 바로 “local invariance”를 유지를 해야한다는 것입니다.

--> spatial 문제점 ?
만약 이웃노드들이 고정되지 않은 상황인 경우에는 (특히 이웃 노드들도 이웃 노드들의 이웃으로 인해서 update 된다면?
한 노드 안에 혼재된 signal들을 여러 signal 요소로 나눈 뒤 node의 특징을 추출하자 --> spectral GCN의 시작
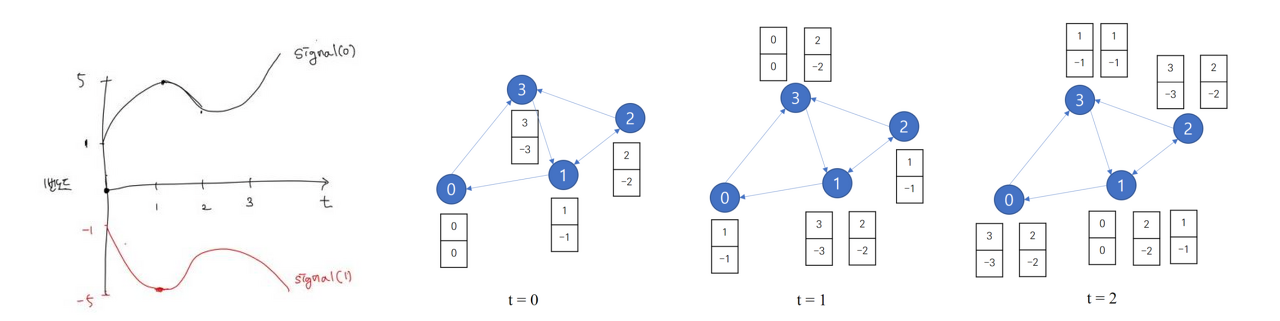
## Spectral
graph signal을 Laplacian Matrix로 표현한뒤 고유값 분해


1. Spectral GCN은 signal processing (SP)에서 사용하는 Fourier transform을 활용하여 convolution theory와 연결하여 사용한다.
2. Fourier transform을 위해 사용하는 것이 Laplacian operator이다.
3. Graph Laplacian operator는 두 노드간의 거리를 나타내는 방법이다.
4. Laplacian matrix에 eigen decomposition을 사용하여 eigenvalue와 eigenvector를 활용한다.
(localized한 피쳐를 활용 가능함과 동시에 마치 Marix Factorization과 같은 효과)
5. Fourier transform에 사용하는 eigenvector를 Laplacian matrix에서 구한 eigenvector로 사용한다.
6. Convolution은 Fourier transform의 곱과 같으므로 convolution 연산을 Fourier transform을 활용하여 계산할 수 있다
2. Graph neural network의 구성요소

1) Adjacency Matrix
- 노드들 간의 연결 여부 1/0 혹은 연결 강도로도 표현
- 위 그림의 예시로 보자면, 1번 node는 2번과 3번 node에 연결이 되어 있으므로, 행렬의 첫 번째 row와 column에 [0, 1, 1, 0, 0]
- node가 N개일때 Adjacency Matrix 행렬의 사이즈는 N x N
2) Node Feature Matrix
각 노드의 feature 정보 - 같은 노드의 피쳐는 같게 표기됨 (빨강, 노랑))
ex. 하나의 노드가 user 라면 성별, 나이, 가입년도 등등
3. GCN = GNN + CNN
왜 하필 CNN?
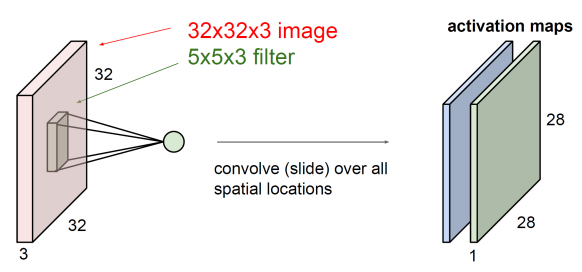
CNN의 특징
- weight sharing 한다 (하나의 filter가 한 이미지를 이동하면서)
- 파라미터 개수를 축소, 컴퓨팅파워 줄임
- local feature extraction 가능
GNN 에 적용한다면 ?
- Node feature matrix 에 CNN filter를 적용해보면? 그래프의 weight를 업데이트한다는 목적으로
- 즉 각각 노드의 정보 (node feature matrix의 row)를 업데이트 한다.
어떻게 업데이트 ? CNN 처럼 그 주변에 있는 정보들만 활용해서 업데이트를 하자
4. spatial GCN

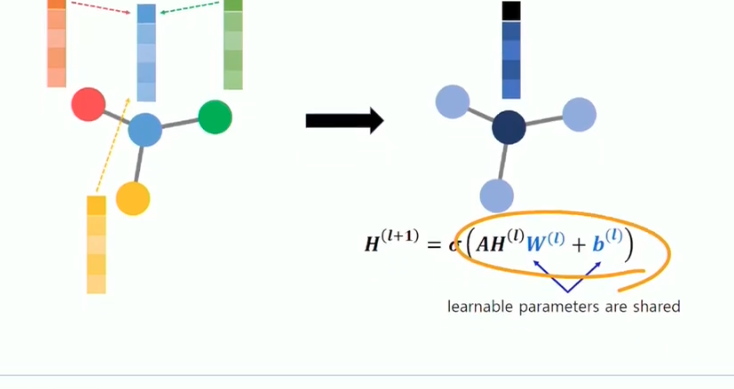

* 수식 해석
0번째에서 1번째로 넘어갈때 1번과 연결된 각각의 노드 H1, H2, H3, H4에 동일한 weight W(0) 을 곱한뒤
activation fuction 시그모이드를 통과시키고 1번째로 넘어감
→ 이때 중심 노드와 연결되어있는 노드만 연산함으로써 local 한정보만 뽑아냄
→ 연결된 노드들 간의 weight는 sharing
→ 즉, CNN의 컨셉 가져옴
1) Adjacency matrix

2) Feature matrix

3) weight matrix (10으로 임의로 설정 - 64,128 등등 - hyper parameter)

→ A*H(l)*W(l)

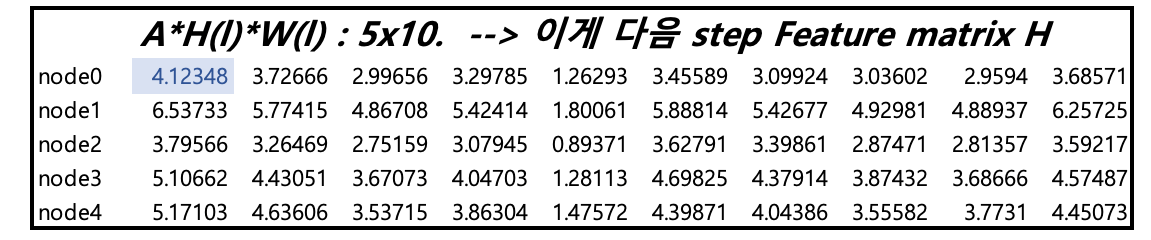
- 4.1235 값은 노드 0 에 대해서 다른 노드(1,2,3,4) 들의 H*W 값들이 반영된 것임
- 내적할때 0과 연결되어 있지 않은 2,3 노드 Adjacency matrix 값은 0이므로 2,3 노드는 반영되지 않음
→ 결국 Adjacency matrix 와의 내적을 통해 해당 노드와 연결 되어있는 다른 노드들의 H*W 값의 합으로 최종 값이 나옴
→ 자기 자신의 값은 항상 1로 연결되어서 다음 hidden state로 전달
- 두번째 Feature matrix H(l+1)의 shape은 현재 node수 * 이전 단계 weight matrix W(l)의 hidden layer개수 --> 5*10
+) Readout layer


사실 위아래 노드 그림은 같지만 매트릭스 표현에서는 다르게 표현될 수 있음
이를 방지하기 위해 readout layer
→ 그냥 denselayer 쌓은뒤 모든 벡터 summation → 각 노드에서 embedding된 값을 합해버림 → activation function 통과
+) overall structure spatial GCN

1) graph conv layer 1,2,3
여러개의 graph convolution layer를 거치며 weight matrix와의 연산을 통해 Feature matrix를 재구성함
2) Readout layer : dense layer 통과 시킨뒤 n차원으로 임베딩 한 후 모든 vector 합하고 activation function 통과
3) Predictor : classification 이라면 cross entropy 로 loss, regression 이라면 MSE로 loss
5. Spectral GCN
참고 link : https://baekyeongmin.github.io/paper-review/gcn-review/
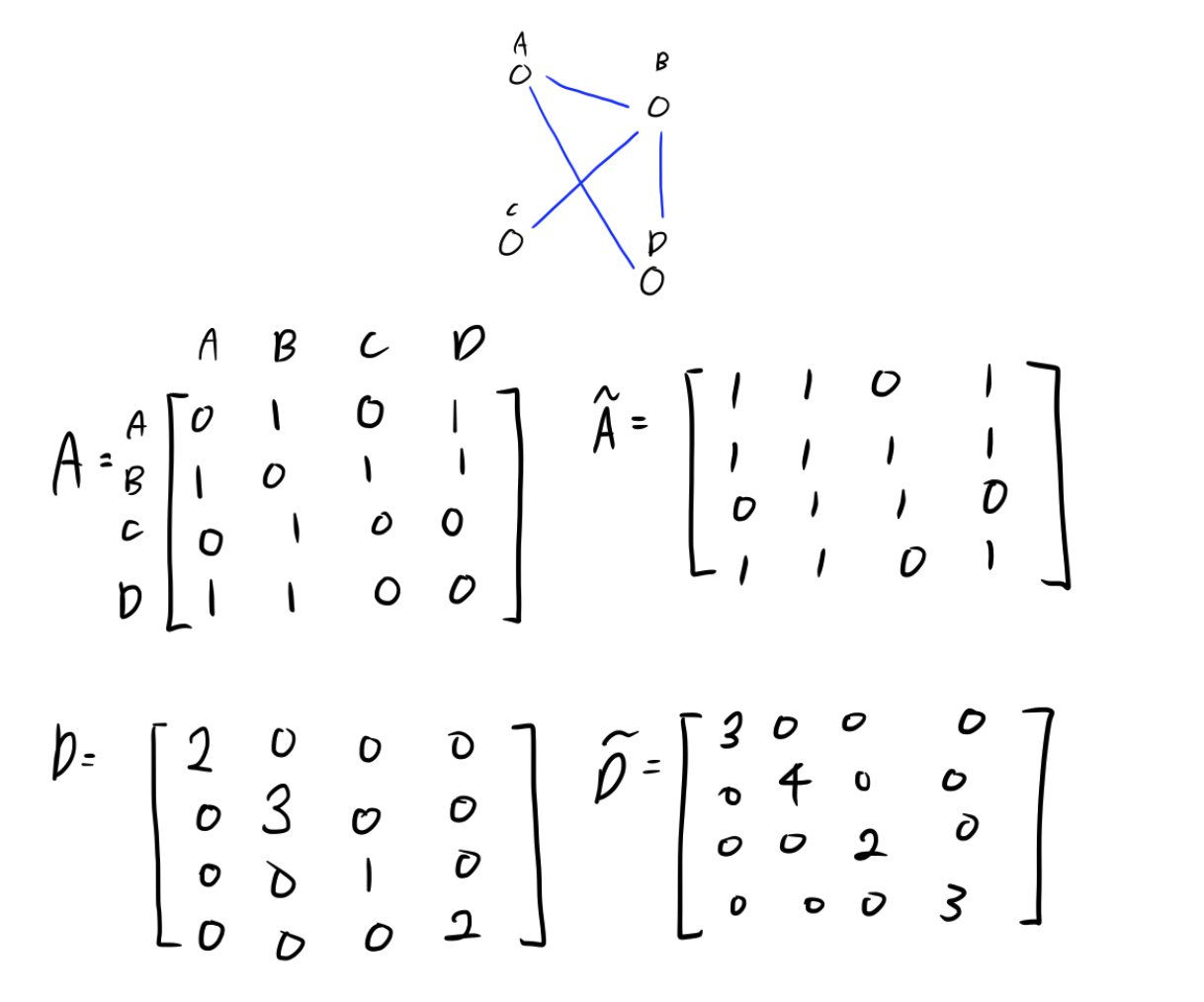

1) ~A
A(인접행렬)에 identity matrix를 더하여 node 자체의 정보를 사용할 수 있게 됐다.
이를 적용하지 않으면 자신의 특성을 고려하지 않고 연산을 수행하는 것과 같음
2) ~D
연결이 많이 된 node일수록 연산 이후 큰 값을 가지게 되고 적게 연결 될수록 작은 값을 가진다.
--> 따라서 degree matrix를 이용하여 normalization을 수행
--> 이는 exploding/vanishing gradient 현상을 방지하기 위해 사용
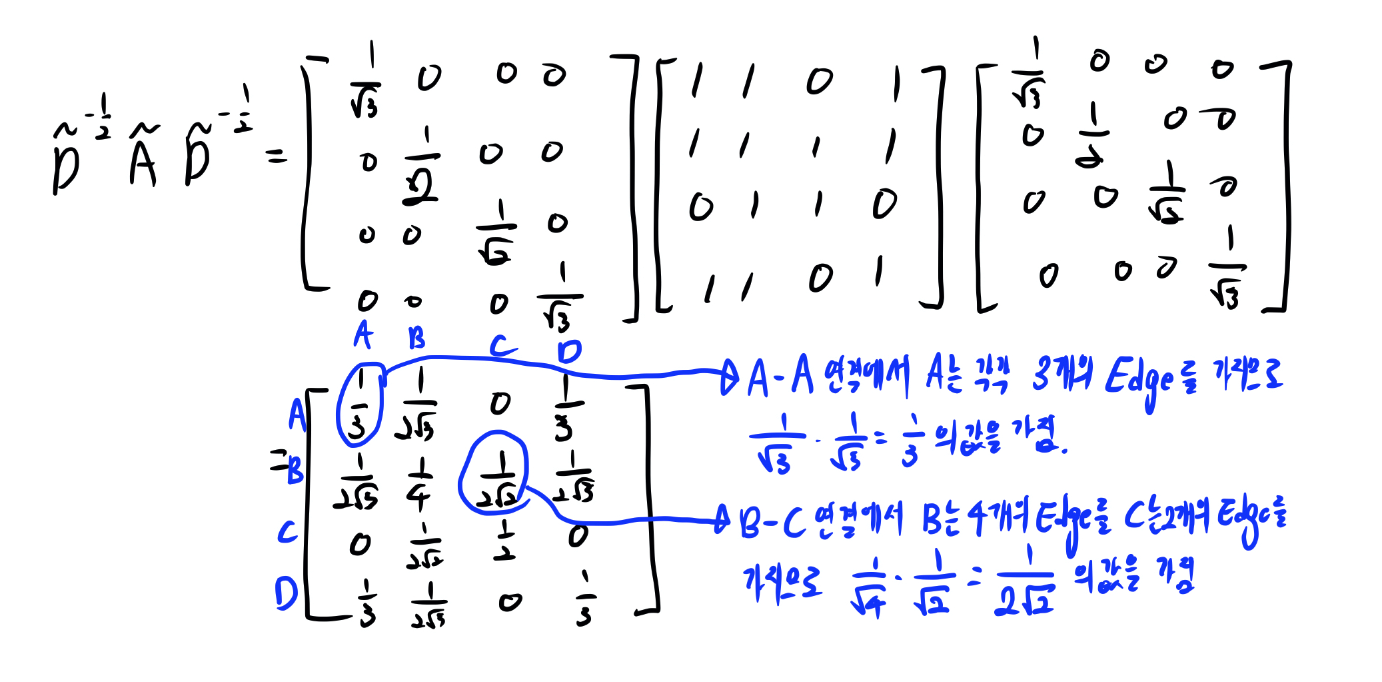
각 노드에 연결된 edge의 갯수에 따라 인접행렬(A)을 정규화(normalization)
이는 학습을 진행할 때, 각 노드별 edge의 갯수에 관계없이 모든 노드들을 잘 학습하기 위한 과정으로 볼 수 있음
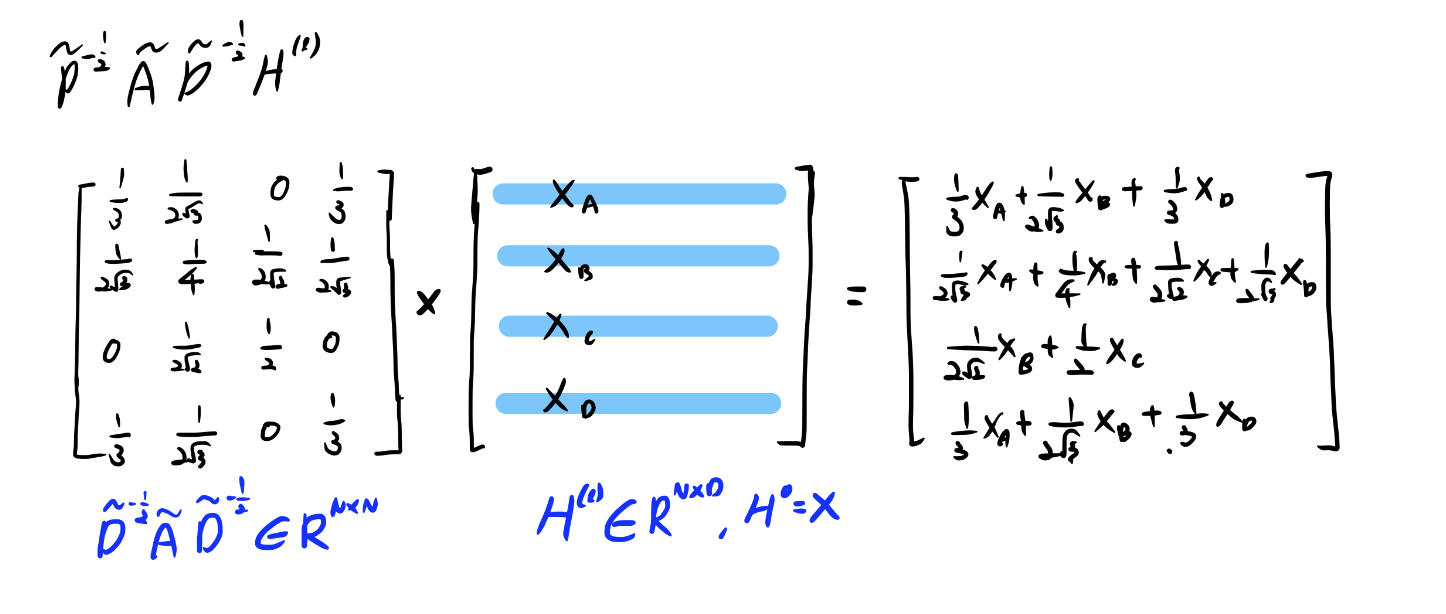

6. Experiments (GCN 논문에서 나온)

1) Dataset
- Citation Network Dataset : Citeseer, Cora, Pumed
- Knowledge Graph dataset : NELL
Node : Documents
Edge : Citation link
Label rate : 각 데이터셋에서 훈련에 활용되는 Training node를 전체 노드 개수로 나눈 비율
Node Feature : Bag of word
Label : Node Label (어떤 종류의 논문인지에 대한 Label) Multi class classification
2) Performance
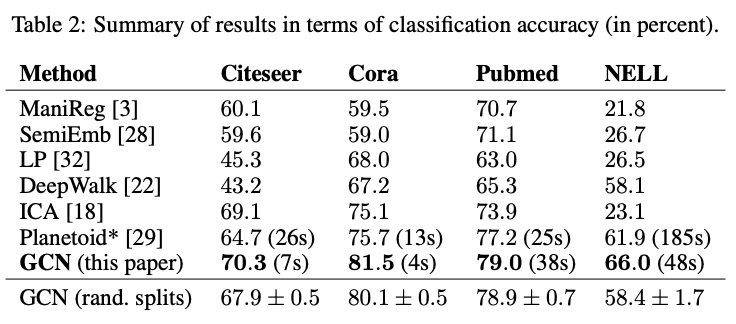
- GCN이 이전 Graph neural network 모델들에 비해 우수한 성능을 보임 - accuracy 기준
#### 논문에서 나오는 컨셉 (상세 설명 참고 link : https://www.youtube.com/watch?v=F-JPKccMP7k)
Fourier Transform, Convolution Theorem
Spectral VS spatial, Laplacian
Chebyshev Polynomials, Layerwise Linear model
#### GCN 실습 코드 설명 - 분자 구조 graph Molecular Property(logP) Prediction
https://www.youtube.com/watch?v=htTt4iPJqMg
### 추천 알고리즘 pinSAGE
1) base GCN
2) GraphSAGE : GCN mini batch 추가 적용, Neiborhood sampling 기법 추가 (transductive, inductive)
3) GAT : Graph attention network: 이웃 통합시에 가중치 부여에 대해서
4) pinSAGE : Graph sage에서 Bi-partite 구조에 적용
https://www.youtube.com/watch?v=y52qSiGOhbs
#### 참고 link
spectral, spatial : https://ralasun.github.io/deep%20learning/2021/02/15/gcn/
GCN - laplacian : https://ahjeong.tistory.com/14
댓글