지난 포스팅들에 이어서 VAE (Variational Autoencoder)를 활용한 추천 알고리즘을 살펴보려한다.
그중에서도 이번에 볼 논문은 mult-vae라고 불리는 " Variational Autoencoders for Collaborative Filtering" 논문이다.
[ index ]
pre. AutoEncoder과 Recommendation system
------ 논문 내용 -----
1. Introduction
2. Method
3. Related Work
4. Empirical Study
pre1. AutoEncoder과 Recommendation system
Autoencoder를 추천시스템에 쓰는 이유는?
1. 차원 축소 - matifold learning (basic AE)
상품, 콘텐츠의 메타정보가 포함된 matrix를 dense 한 latent space 로 압축 (Embedding)
latent space를 추출해서 contents 간의 similarity 계산할 수 있음
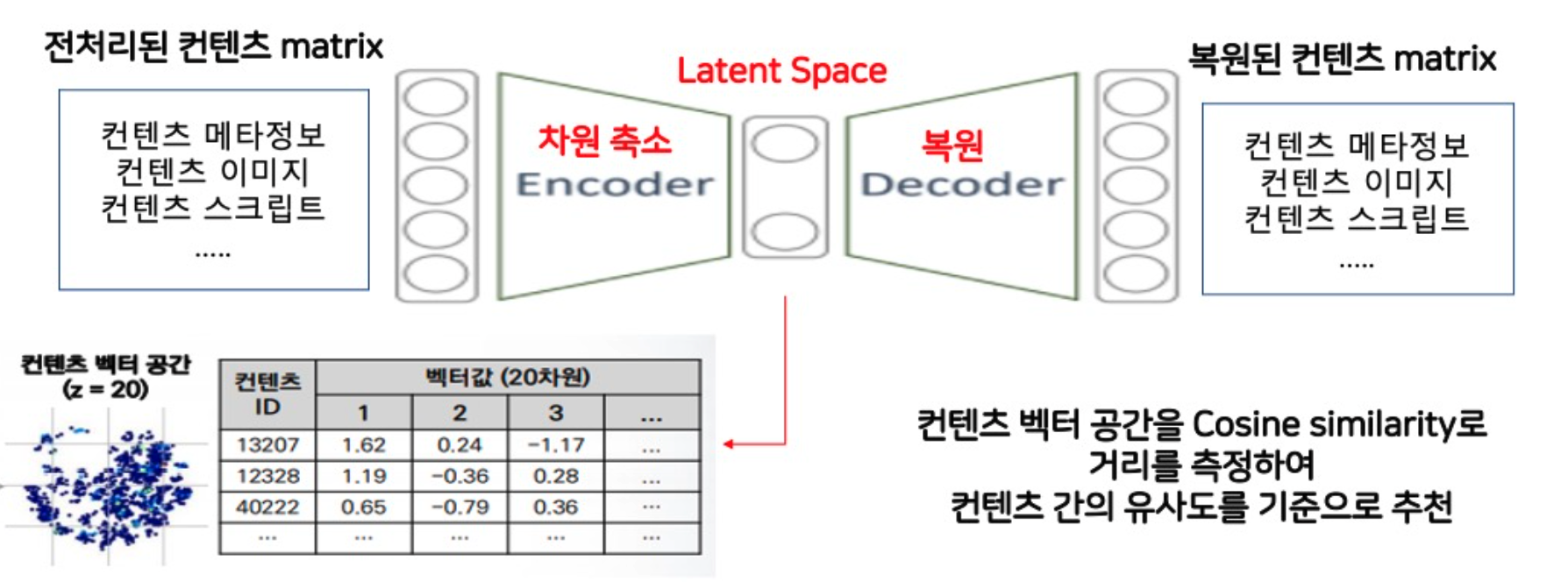
2. 복원 및 생성 - generative learning (AE, VAE, DAE)
input X를 output X로 복원하는 과정에서 특정 user에 대해 예측해내야 하는 item의 rating을 생성해낸다

현재 추천 알고리즘 중에서 Autoencoder를 기반으로 한 모델은 ?
CDAE : Collaborative denoising auto-encoders for top-n recommender systems (2016)
Mult-DAE, Mult-VAE : Variational Autoencoders for Collaborative Filtering (2018) <--- now !
RaCT : Towards Amortized Ranking-Critical Training for Collaborative Filtering (2020)
RecVAE : a New V
ariational Autoencoderfor Top-N Recommendations with Implicit Feedback (2020)
우리가 이번에 살펴볼 논문은 Mult-VAE 가 소개된 "Variational Autoencoders for Collaborative Filtering" 논문이다.
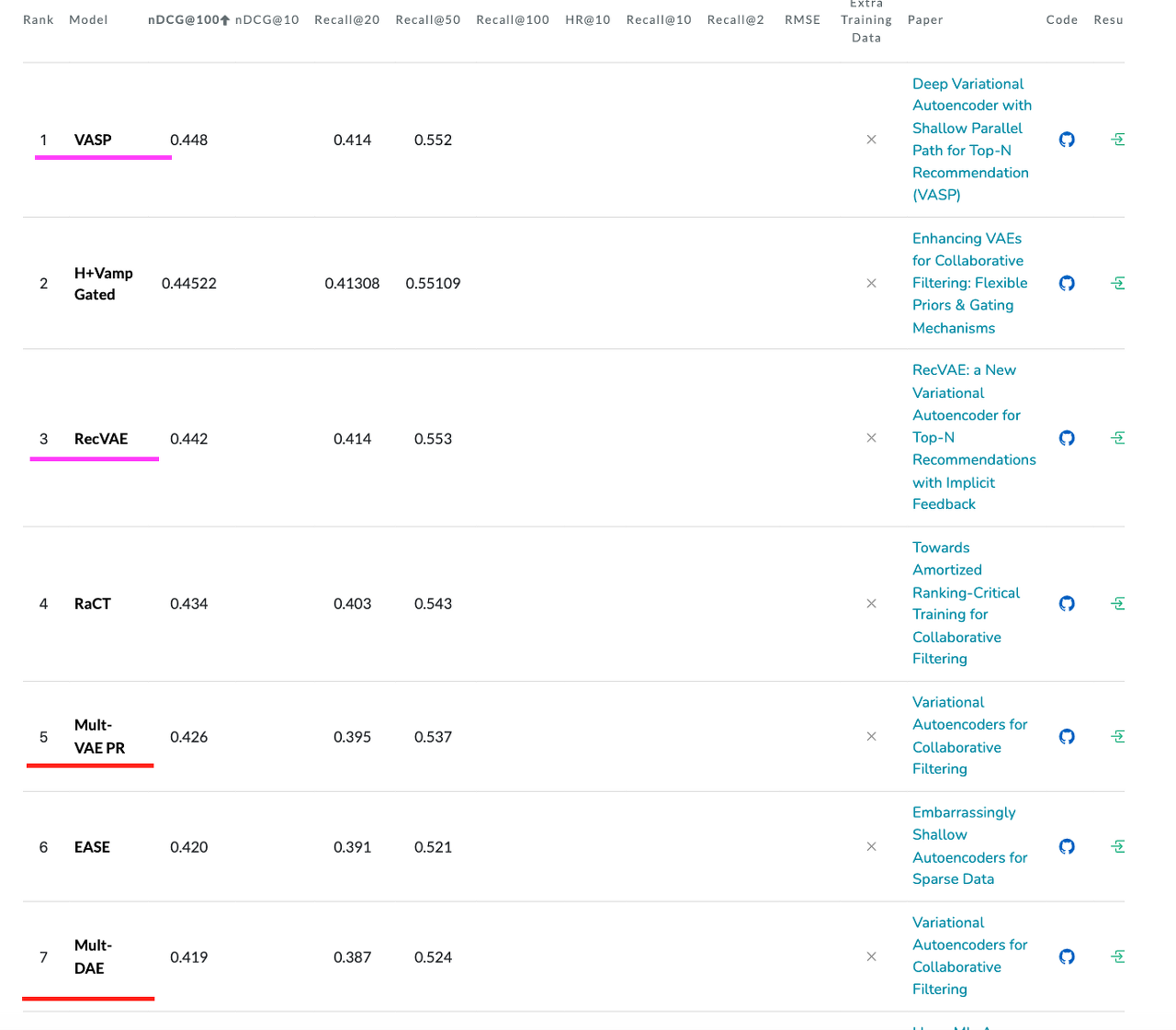
paper with code에서 MovieLens 20M 데이터 기준으로 봤을때 많은 AE기반 모델들이 순위에 랭크된 걸 확인할 수 있다.
(1k 에는 그래프 기반 모델들이 우수한 성능을 보이고 있다)
1. Introduction
[ contributions ]
1) Multinomial likelihood 사용
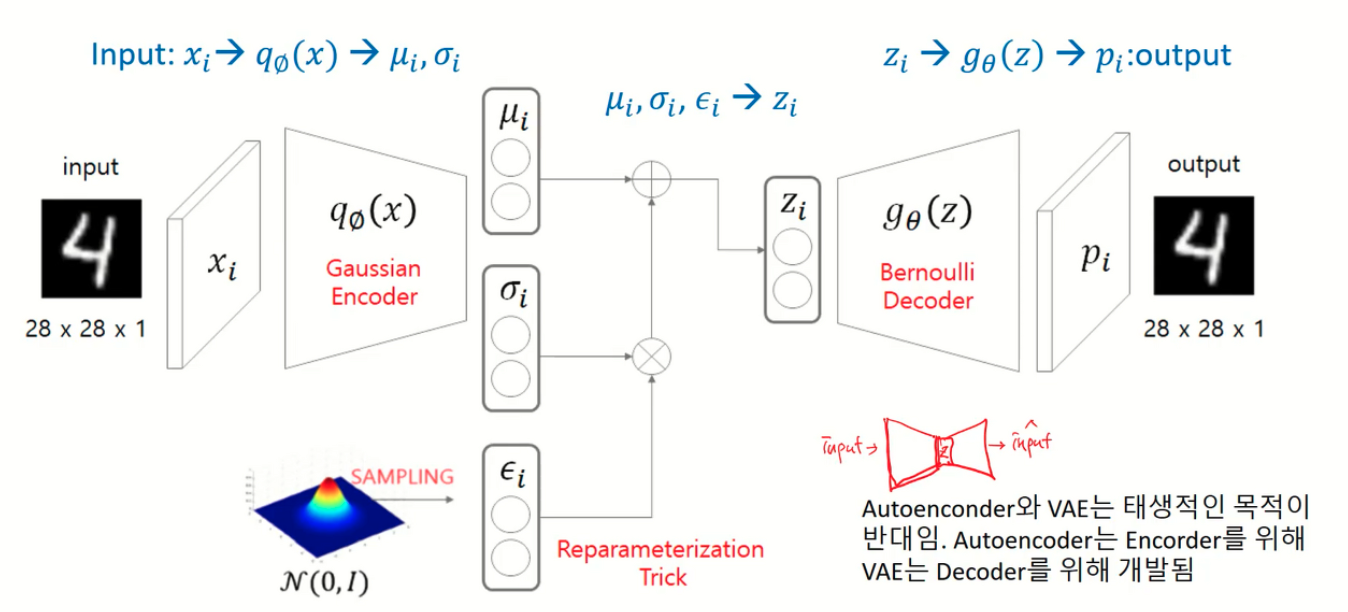
기존 VAE 모델에서는 encoder에서 gaussian distribution을 가정하고, decoder에서 bernouii distribution을 가정하지만,
mult vae 모델에서는 decoder 부분이 베르누이가 아닌 다항분포 (Multinomial distribution) 을 따른다고 가정하는 것
2) regularization term 수정

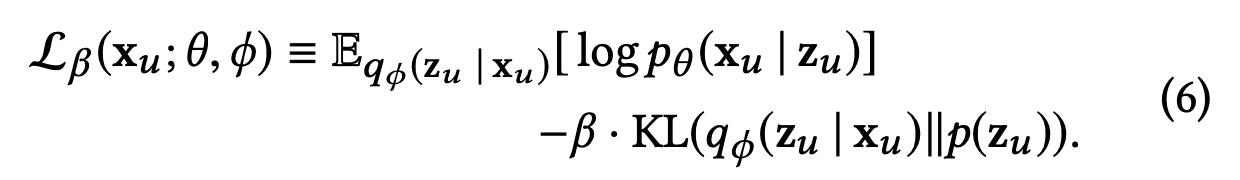
기존 VAE 모델 목적함수는 over-regularized 되었다고 판단
Loss 에서 regularizationterm 의 영향을 줄이기 위해 1보다 적은 수인 베타를 곱함
ex. Reconstruction Error = 3, KLdivergence = 2, Beta = 0.5
basic VAE Loss : 5 /// Mult VAE Loss : 4
2. Method
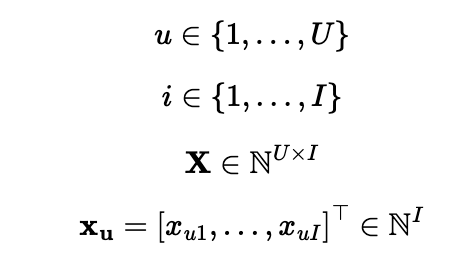
- u : user
- i : item
- Xu : user u의 각 item(1~I) 에 대한 벡터
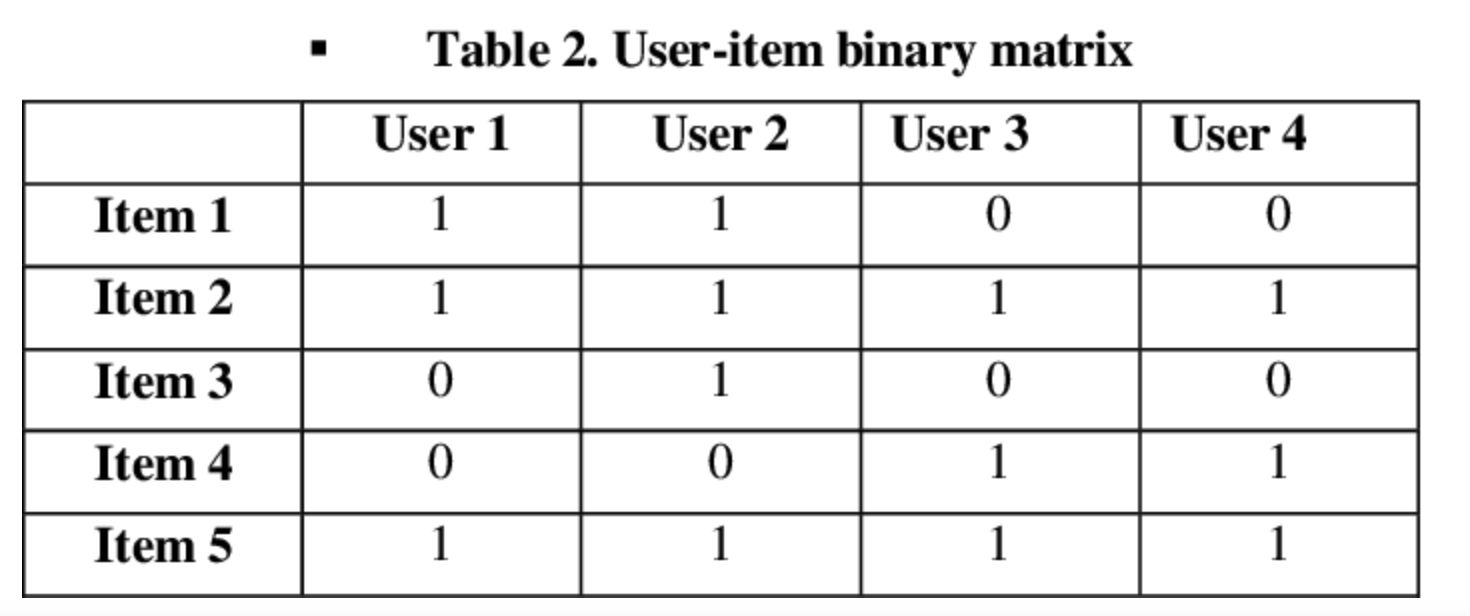
- X : user과 item의 interaction matrix (아래와 같은 bag-of-words 형태로 표현됨)
matrix shape = (item 수, user 수)
2.1. Model
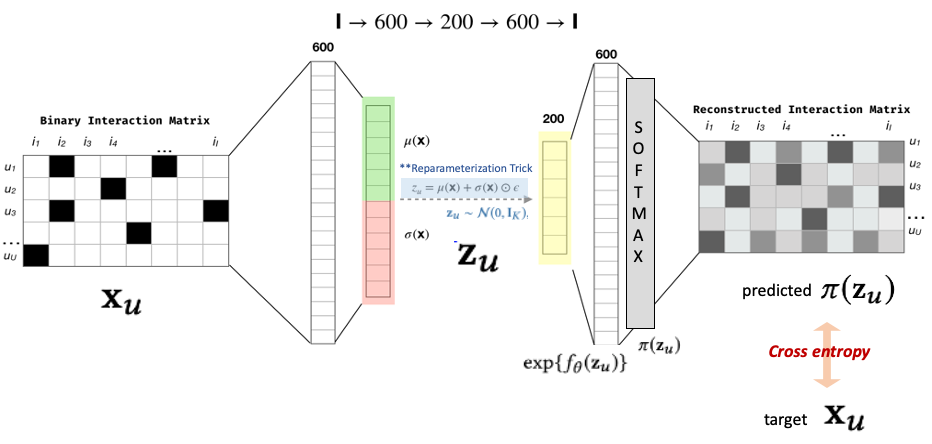
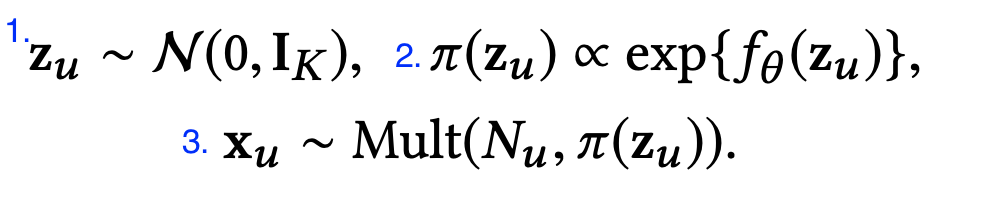
1. 기존 VAE 에서처럼 해당 논문에서도 Encoder를 거친 Zu는 표준 정규 분포 (Standard Gaussian) 를 갖게됨
2. non-linear function fθ(⋅) 은 파라미터 θ 를 가지는 FCNN Layer
-> 여기에 softmax 적용 (exp 취해서 벡터값 0~1 값으로 바꿈 normalize)
이 softmax output 값은 π(Zu) 과 비례하며 π(Zu)는 전체 아이템에 대한 해당 유저의 확률 벡터로 해석 할 수 있다.
3. Zu (latent vector) 를 다시 decoder로 태울 때 Multinomial distribution (다항분포) 이라
가정
기존 VAE : Decoder (bernoulli distribution) 이항분포 - binary classification 문제 --> sigmoid - binary cross entropy
+ (Gaussian distribution) 정규분포 - regression 문제 --> squared error
multVAE : Decoder (Multinomial distribution) 다항분포 - multi-class classification 문제 --> softmax - cross entropy
[ bernoulli - sigmoid VS Multinomial - softmax output ]
ex. x1 = [-0.5, 1.2, -0.1, 2.4]
sigmoid output = [ 0.37, 0.77, 0.48, 0.91]
softmax output = [ 0.04, 0.21, 0.05, 0.70]
sigmoid : 한 X1에서 각 인스턴스의 값이 독립적임
--> 추천 basic VAE : 한 유저에 대한 각 아이템들의 예측 평점이 독립적임 (각각 선택할 확률)
softmax : 한 X1에서 각 인스턴스의 값이 상대적임
--> mult VAE : 한 유저에 대한 각 상품들의 예측 평점이 상대적임 (랭킹, 순위)
4. 다항 분포에 대한 loss function - cross entropy
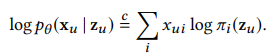
- 위와 같은 Loss를 사용하면 Multi-VAE라고 부름
- multi-class classification을 위한 cross-entropy loss로 볼 수 있음
- 는 output인 reconstuct x에 softmax 함수에 통과시킨 probability vector임
- 그러나
2.2. Variational inference
# KLterm - annealing
[ 기존 VAE loss function ]

[ mult VAE loss function ]
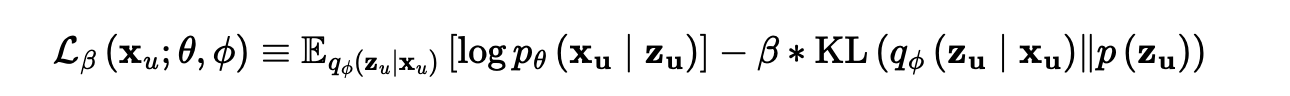
- Multi-VAE의 목적함수는 기존 VAE와 달리 KL term에 β를 추가
- 베타 값이 작을 수록 KLterm이 Loss에 미치는 기여 작아짐, Reconstruction에 focus
- 파라미터 β를 선택하는 과정은 heuristic하게 0부터 시작하여 1까지 점진적으로 증가시키면서 β를 탐색 ==> KL annealing
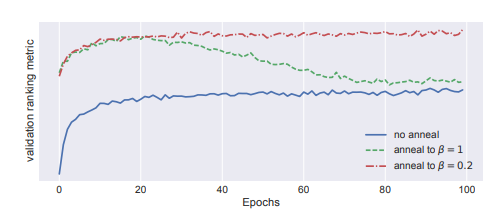
- 파랑 - annealing 이 없는 경우는 성능 향상이 되지 않음
- 초록 - 1까지 탐색했을 경우 파란색보다는 성능 향상이 다소 됨 그러나 에폭이 증가할 수록 성능이 떨어짐
- 빨강 - 최적의 베타를 계산한 후 베타 값을 고정시키고 베타 값 증가를 중단함 (0.2에서 더 오르지 않음)
- annealing 과정은 VAE를 학습하는데 있어서 추가적인 runtime를 발생시키지 않음
2.3. A taxonomy of autoencoders
# DAE
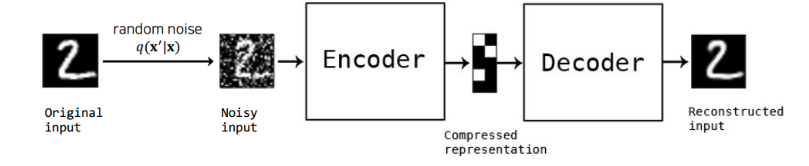
- DAE는 입력데이터에 일부러 노이즈한 input을 만들기위해 random noise나 dropout을 추가하여 학습
- 이 input(noisy input)을 잘 복원할 수 있는 robust한 모델이 학습되어 전체적인 성능향상을 한다는 것이 DAE의 핵심
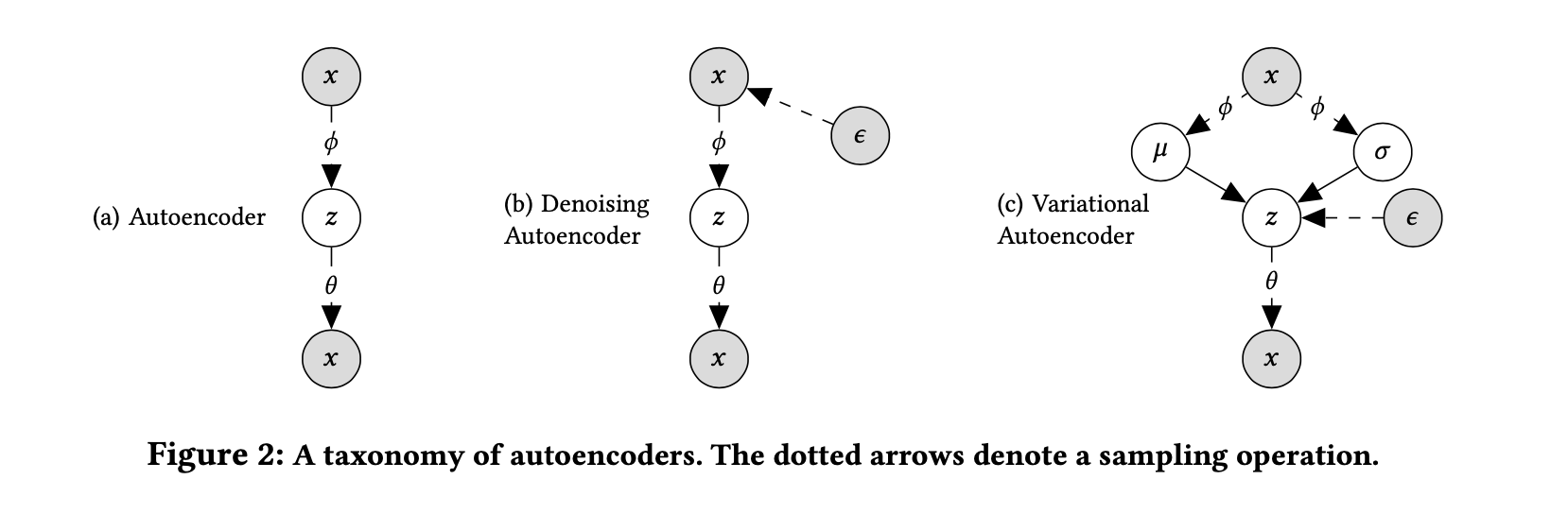
# mult DAE
- Mult DAE : DAE concept + variational autoencoder
- 기존 variational autoencoder 식에서 Ep(x ̃ |x) noise 항을 곱함

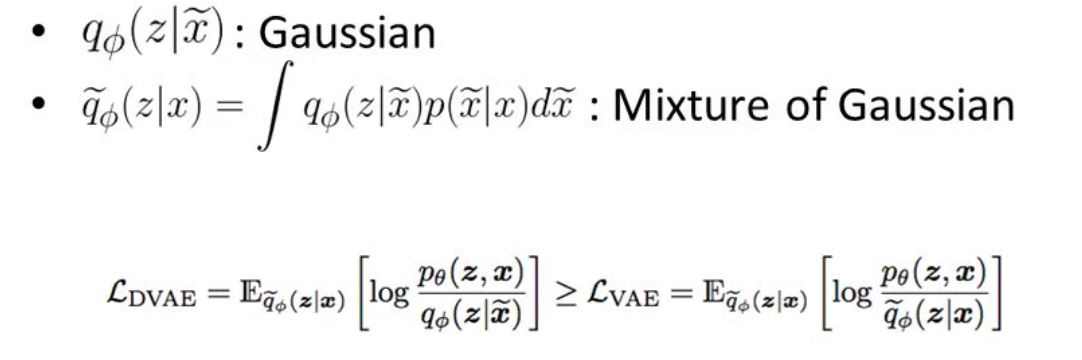
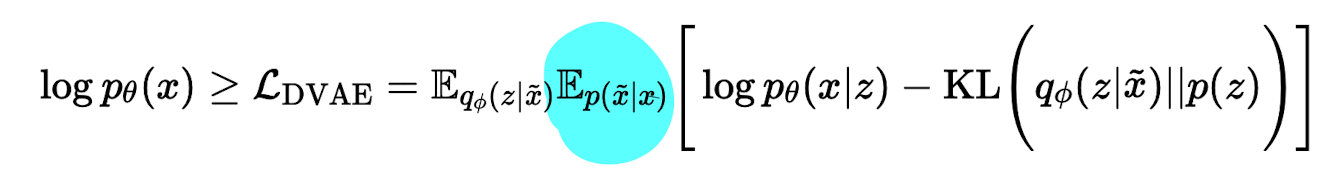
- VAE에서 prior를 근사하는 variational distribution (즉 encoder의 output) $q_{\phi}(zu|xu)$ 을 정규화하지 않는다.
- 즉 qϕ(zu∣xu)=δ(zu−gϕ(xu)) 를 통해서 optimize 됩니다.
2.4 Prediction
Mult-VAE와 Mult-DAE 모두
유저의 click history x가 주어지면 multinomial probability fθ(z)를 구함 --> 모든 아이템에 rank를 매김
Mult-VAE 경우, z는 variational distribution의 평균, z=μϕ(x)
Mult-DAE 경우, z는 embedded vector, z=gϕ(x)
결국 z를 분포로 나타내기 위해 평균을 사용할지 하나의 single value로 나타낼지의 차이
3. Related Work
1) Vaes on sparse data
최근 연구들에 의하면 VAE는 large, sparse, high-dimensional 한 데이터를 모델링 할 때 underfitting 됨
논문에서도 annealing을 수행하지 않거나 β=1로 설정할 경우, 비슷한 이슈 발생
따라서 ancestral sampling을 수행하지 않고 β≤1 로 설정하게 되면 적절한 generative model이 아닐수도 있지만
collaborative filtering 관점에서 항상 유저의 click history에 기반하여 예측
2) Information-theoretic connection with VAE
위에서 정의한 ELBO의 regularization term은 Bayesian inference와 generative modeling을 통해서 Maximum-entropy discrimination을 수행하며, β는 모델의 discriminative와 generative의 부분을 조절하는 역할
다시 말하면 VAE 모델은 유저의 click history를 기반으로 최대 엔트로피를 가지는 분포를 찾는 것이며,
이 떄 β를 통해 prior를 얼마나 반영할지를 조절할지를 결정하는 파라미터
3) Neural networks for collaborative filtering
초기 neural network기반의 CF모델들은 explicit feedback의 데이터와 rating을 예측하는 것에 집중
최근에는 implicit feedback의 중요성이 높아져가면서 그에 대한 연구들이 진행
이에 대해 우리의 연구와 관련된 중요한 논문들은 CDAE 와 NCF
모두 유저와 아이템의 수에 따라서 모델의 파라미터가 점진적으로 증가하기 때문에
이는 larger datasets에서는 문제가 될 수 있음을 파악하고 각 데이터셋에 대해 실험
4. Empirical Study
Mult-VAE 와 Mult-DAE 두 모델에 대한 성능을 측정
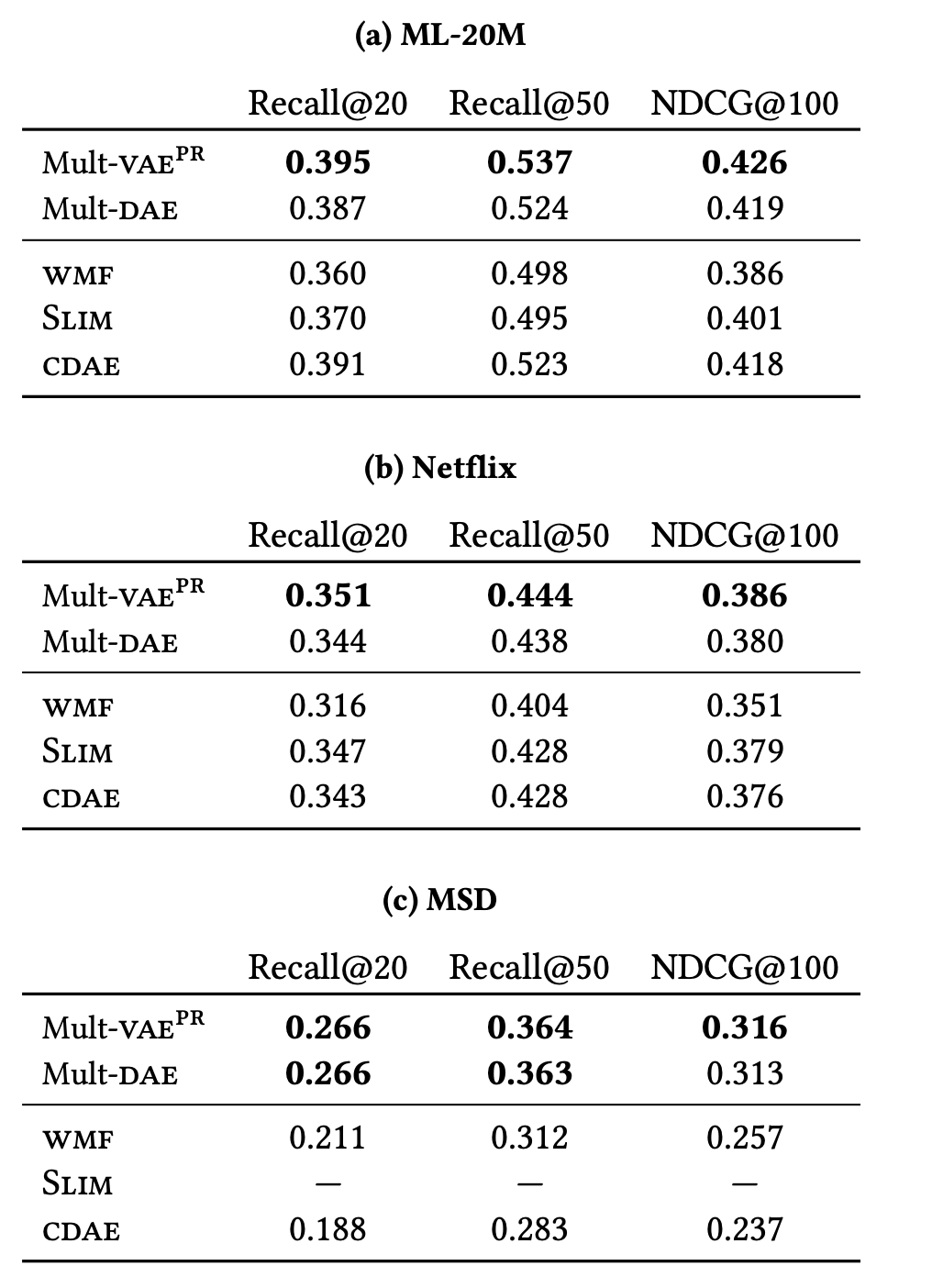
- Mult-VAE은 최근에 제안된 neural-network-based CF 모델들보다 SOTA성능을 달성
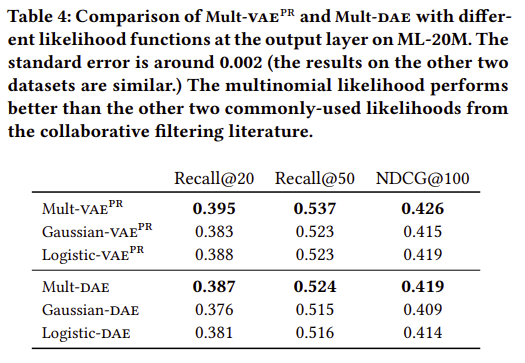
- DAE와 VAE에서 multinomial likelihood를 사용하는 것이 다른 Gaussian이나 logistic likelihoods보다 더 나음
- Mult-VAE와 Mult-DAE를 비교하였을떄, 항상 특정 모델의 성능이 높게 나오지는 않음 - 각각의 장단점 있음
4.1 Dataset
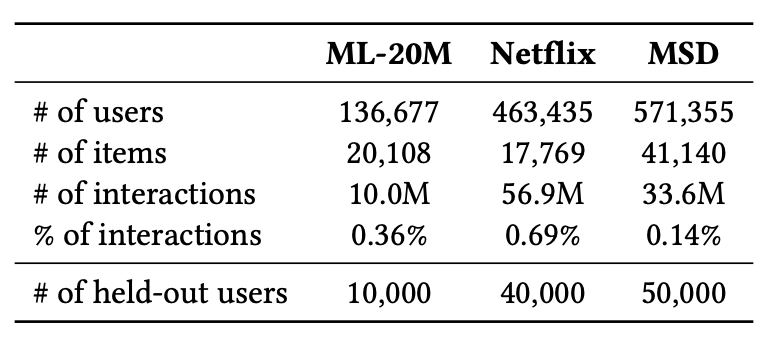
- MovieLens-20M (ML-20M)
- Netflix Prize (Netflix)
- Million Song Dataset (MSD)
4.2 Metrics
Recall@R, NDCG@R 두 개의 rank metric을 사용해 성능을 평가
각 유저에 대해서 클릭한 아이템에 대한 predicted rank와 true rank를 비교
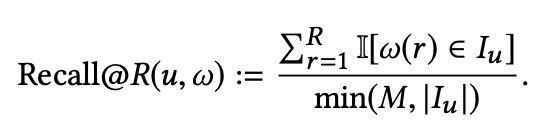
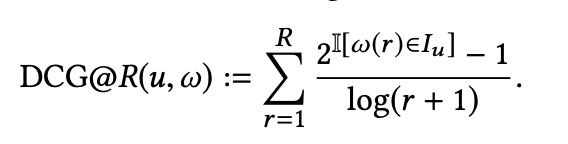
ω(r) 은 아이템에 대한 rank r 이며,
I[⋅] 는 indicator function,
Iu 는 유저가 click한 held-out 아이템들의 집합
1) Recall @ K
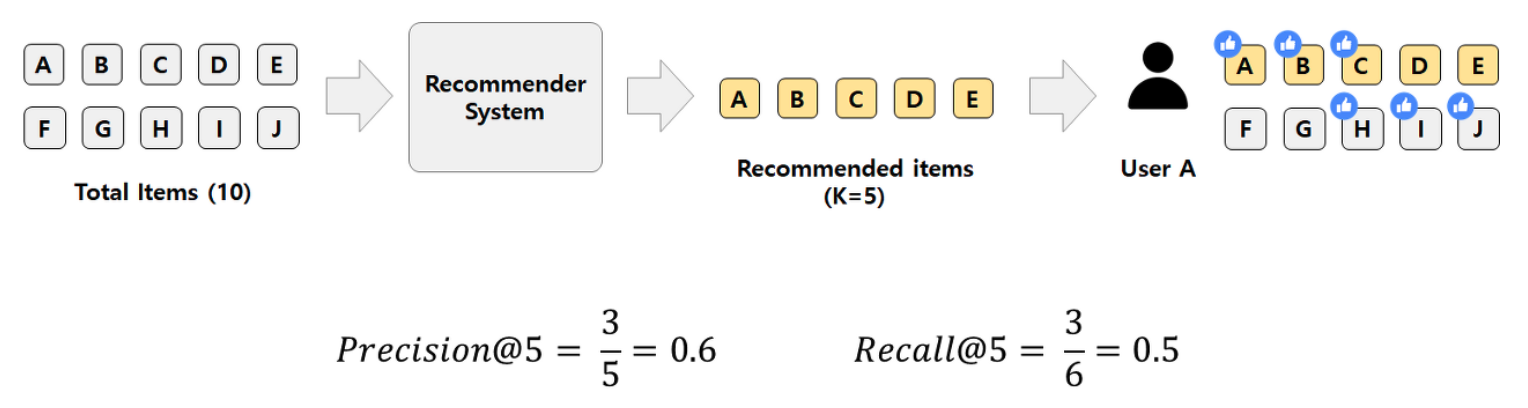
Recall은 실제 모든 1 중에서 내가 1로 예측한 것이 얼마나 되는지 비율
Recall@K는 사용자가 관심있는 모든 아이템 중에서 내가 추천한 아이템 K개가 얼마나 포함되는지 비율
예시를 보면, 사용자가 좋아한 모든 아이템이 6개, 그 중에서 나의 추천에 포함되는 아이템이 3개다.
Recall@5=0.5
2) NDCG
현재 DCG값에서 이상적인 DCG 값(=IDCG) 나눈 값, 최대값은 1 (예측 DCG = IDCG)

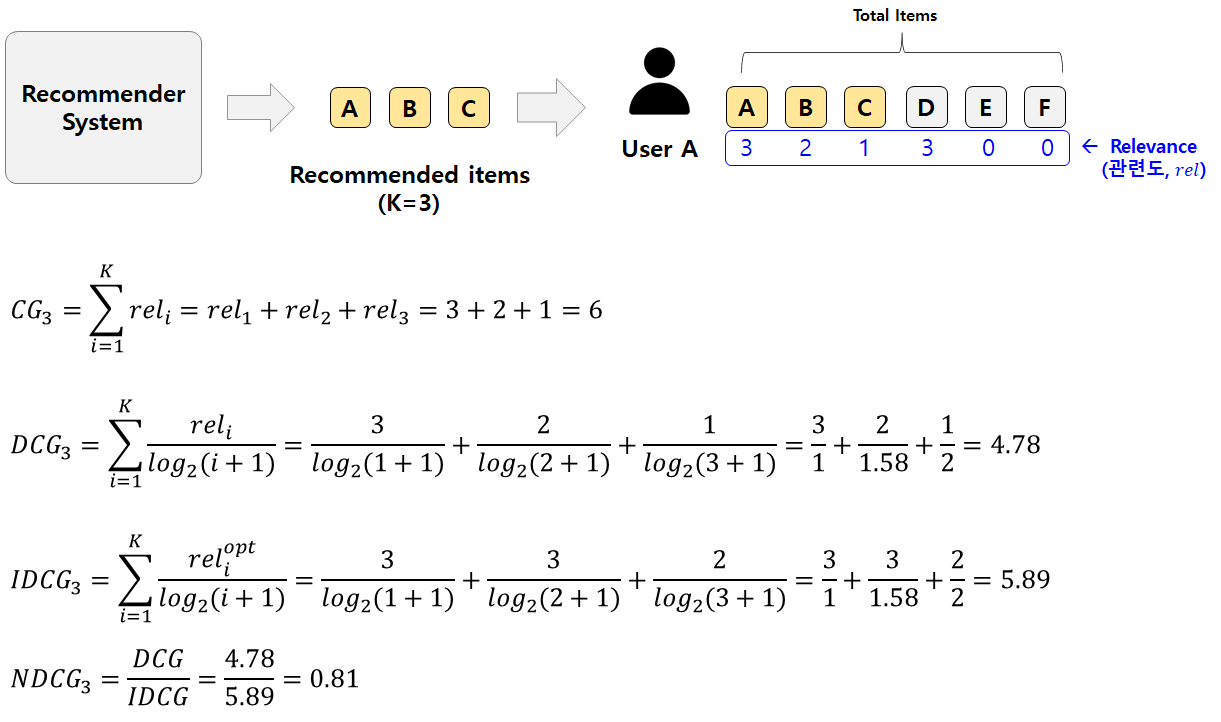
4.3 Experimental setup
- strong generalization를 위해서 모든 유저들을 training / validation / test sets으로 split
- validation and test의 경우, user들의 전체 click history가 아니라 모델이 필요한 user-level representation을 학습하기 위한 click history의 일부분만을 이용하여 평가 --> unseen click history도 잘 평가하는지 판단하기 위해
- validation users에 대한 NDCG@100를 기반으로 모델의 hyperparameter와 architectures를 선택
- Mult-VAE와 Mult-DAE 의 전반적인 모델 구조는 1-hidden-layer를 가지는 MLP generative model이며 실험적으로도 0~1개의 hidden layer의 구조가 성능이 우수
vae, dae 공통 setting
- input layer에 대해서 dropout(p=0.5)를 적용
- batch_size= 500
- opimizer = Adam
- ML-20M 데이터셋의 경우, 200 epoch 동안 train
차이점
- Mult-DAE의 경우 input layer에 대해서 tanh activation function을 적용하고 weight decay 수행
- Mult-VAE 는 encoder의 output이 gaussian 분포로 사용되기 때문에 0-hidden-layer MLP 구조가 사용되었음
4.4 Baselines
- Weighted matrix factorization (WMF)
- SLIM
- Collaborative denoising autoencoder(CDAE)
- Neural collaborative filtering(NCF)
4.5 Experimental results and analysis
1) 실험 결과
2) multinomial VS gaussian VS logistic
3) Mult-VAE VS Mult-DAE?
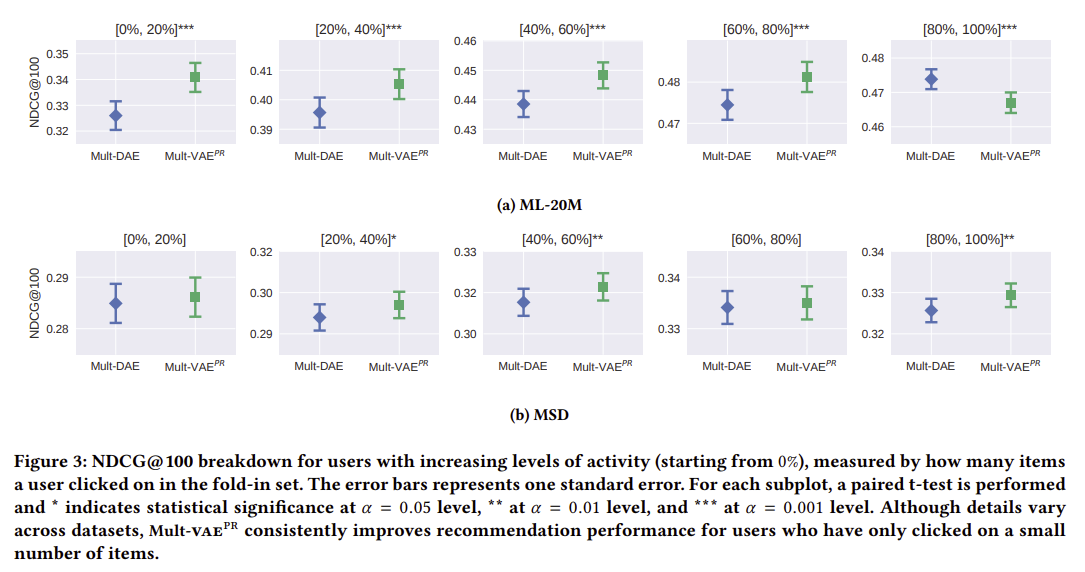
* 실험 환경
- 직관적으로는 interaction 데이터가 희소할때 (부족할때, sparse 할때) mult vae가 더 강력함
- 사용자의 활동량에 따라서 5분위로 그룹핑 한뒤 성능 평가 (0~20, 20~40, ... 80~100)
- 활동량이 높은 사용자들 그룹 데이터로 학습한 모델일 수록 더 좋은 성능을 보임
* 실험 결과 및 해석
- ML20m에서 80-100 그룹에서는 DAE가 성능이 더 높음
-> 이건 많은 데이터가 있을 때 오히려 VAE 접근법 (prior assumption) 이 더 성능을 낮춘다고 해석 가능함
- mult vae는 파라미터 조정에 덜 민감하다 반면 mult dae는 파라미터 조정에 성능이 크게 영향을 받음
(특히 weight decay parameter가 성능에 크게 영향)
- mult dae는 그래도 한개의 parameter를 생성 (z) mult vae는 2개를 생성해야함 (평균, 분산)
따라서 모델의 복잡도 측면에서 봤을 때 mult DAE가 실무에 더 적합함
참고 link :
https://ratsgo.github.io/generative%20model/2018/01/27/VAE/
https://ratsgo.github.io/generative%20model/2017/12/19/vi/
https://pyy0715.github.io/VAE_CF/
댓글