0. 추천 알고리즘의 종류
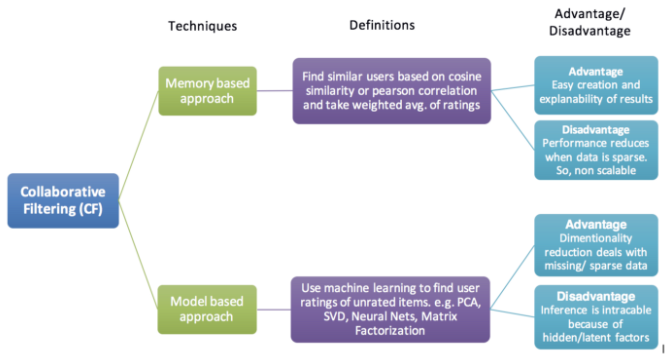
https://towardsdatascience.com/various-implementations-of-collaborative-filtering-100385c6dfe0
1) 협업 필터링(Collaborative Filtering)
• Memory Based Approach : User-based Filtering, Item-based Filtering
• Model Based Approach : 행렬 분해(Matrix Factorization)
2) 콘텐츠 필터링(Contents-Based Filtering)
3) 딥러닝 기반 추천 시스템
1. Memory based algorithm
1) 정의

즉, 사용자 - 아이템 구매 이력을 기반으로 사용자 similarity 혹은 아이템 similarity 구하는 것
사용자 similarity (유저1과 비슷한 제품을 산 유저는 누구인가)
아이템 similarity (아이템1과 비슷한 유저에게 구매된 아이템은 뭔가)
핵심은 user가 각 item을 구매했는지/ 어떻게 평가했는지 에 대한 matrix 가 필요 !
2) Similarity 은 어떻게 계산? cosine similarity
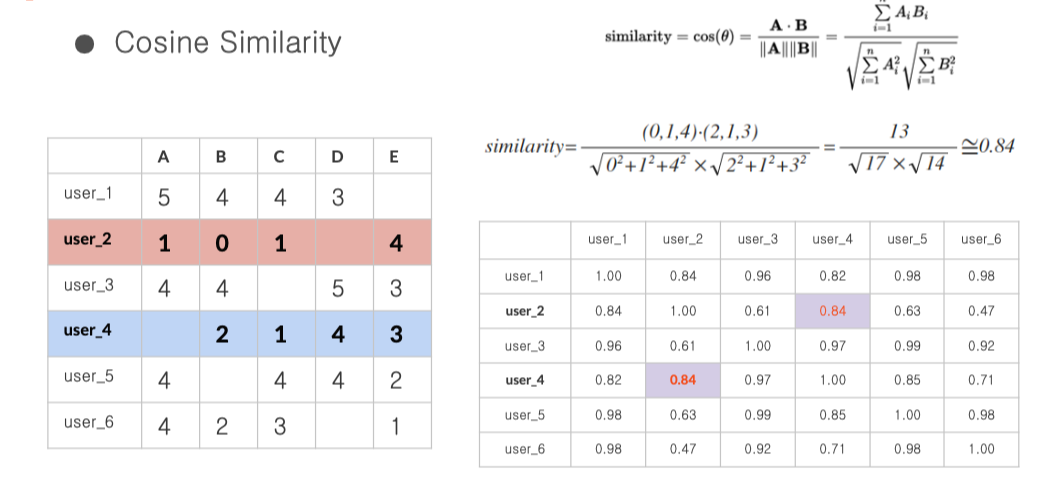
위 장표와 같이 user2, user4를 비교하고 싶다면
user2와 user4 가 각 아이템 별 평가해놓은 데이터를 벡터라 생각하고
두 벡터의 cosine similarity 를 계산
이렇게 각 유저간 cosine similarity matrix 생성 !

3) similarity maxtrix 로 다른 user의 평점 예측 시도


여기서 등장하는 저 값은 어떻게 나왔나?
여기서 중심 유저는 user5
user5 와 user 1의 similarity (=0.98) * user 1의 아이템 B에 대한 평점 (=4)
user5 와 user 2의 similarity (=0.63) * user 2의 아이템 B에 대한 평점 (=0)
user5 와 user 3의 similarity (=0.99) * user 3의 아이템 B에 대한 평점 (=4)
user5 와 user 4의 similarity (=0.85) * user 4의 아이템 B에 대한 평점 (=2)
user5 와 user 6의 similarity (=0.98) * user 4의 아이템 B에 대한 평점 (=2)
의 합이 분자
분모는 모든 유저와의 similairty 합
4) 장단점
:) 구현하기가 비교적 쉽고 추천 생성 시
제품의 콘텐츠 정보 또는 사용자 프로필 정보를 필요로 하지 않음
:( cold start problem - 초기 사용자처럼 사용이력이 없을 때 추천을 하기 힘듦
2. Model based approach

* Memory based 의 한계점 :
cold start problem, 데이터가 sparse함, 확장 가능성이 낮음, 테이블이 커지면 연산 속도 저하
--> 이를 보완하기 위해 등장한게 Model based algorithms
* Model based algorithm의 기본 컨셉
꼭 전체 매트릭스 (user * item) 으로 유사도 구해야하나? 그렇게 하면 차원이 너무 큰데?
- 매트릭스를 행렬분해 해서 차원을 낮추자 --> Matirx Factorization
- 매트릭스를 임베딩해서 차원을 낮추자 --> Deep learning
* Model based CF의 종류
2.1 Matrix Factorization
2.2 Non- parametic Approach
2.3 Deep learning
2.1 Matrix Factorization (행렬 분해)
등장 배경 : 기존의 Memory based 너무 차원이 크고 데이터가 sparse -> 데이터의 차원을 낮춰보자, 행렬을 분해해보자

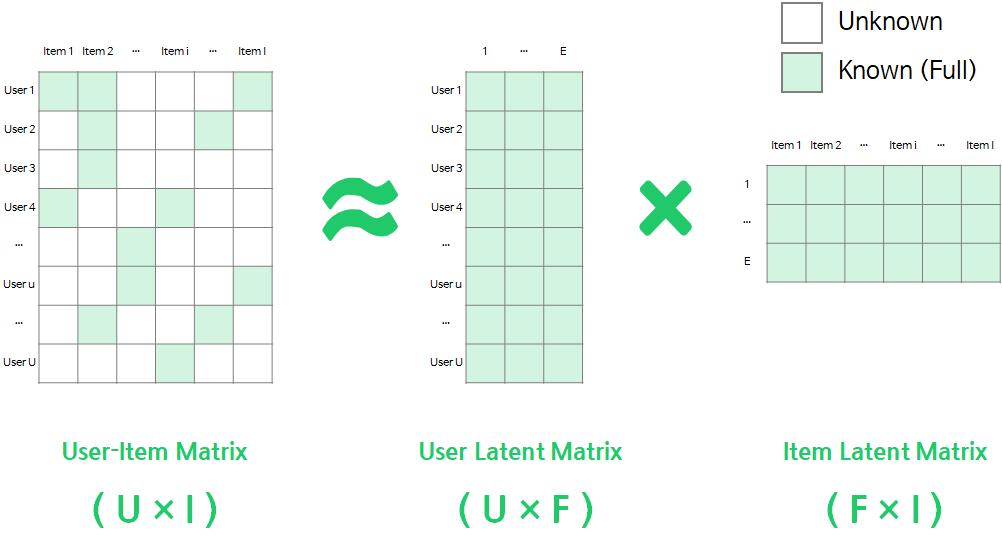
- user - item 에 대한 matrix 좌측의 matrix를 --> 우측의 User latent matrix, item latent matrix 로 분해하는 것
- 여기서 행렬 분해는 SVD (특이값분해), NMF, PMF로 가능함
- 목적은 고차원의 matrix에서 핵심 feature 를 뽑는게 목적 --> 따라서 SVD, NMF 와 같은 차원 축소 기법을 사용
- 이렇게 분해를 하는 이유는 ? User-Item Matrix를 User/Item Latent Matrix로 맵핑(mapping)이 되면,
유저가 평가하지 않은 선호도에 대해서도 위의 수식을 통해 쉽게 추정
- Rating matrix (좌측 4*5 테이블)
: 각 칸에는 유저가 기록한 해당 아이템에 대한 평가가 수치로 기록됨, Sparse 한 매트릭스의 형태
- Rating matrix를 User latent matrix, item latent matrix 로 분해하는데, 각 행렬의 형태는
(1) SVD 로 하는 Matrix Factorization
출처 : https://seing.tistory.com/67

singular value decomposition
| U : 역행렬이 대칭 행렬인 m x m크기의 행렬 left singular matrix로서 User와 latent factor 간의 관계 Σ : 비 대각 성분이 0인 m x n크기의 행렬 diagonal matrix로 각 latent factor의 중요도 (latent factor는 User와 Item이 갖는 특성 VT : 역행렬이 대칭 행렬인 n x n크기의 행렬right singular matrix로 Item과 latent matrix 간의 관계 |
U^ : U에서 k개의 대표 특이치에 대응하는 k개의 성분만 남긴 m x k 크기의 행렬 Σ^ : 대푯값으로 쓰일 k개의 특이치 성분만을 남긴 k x k 크기의 행렬 VT^ : V에서 k개의 대표 특이치에 대응하는 k개의 성분만 남긴 k x n 크기의 행렬 |
여기서 말하는 latent factor는 User와 Item이 갖는 특성을 뜻합니다. --> 즉 feature의 역할 !!
영화라는 도메인을 예로 들자면 latent factor는 장르, 주연배우 등이 될 수 있는데,
여기서 우리는 실제 계산 과정에서 얻어지는 각 latent factor가 무엇을 뜻하는지 유추만 할 뿐 정확한 해석은 불가능.
(2) NMF 로 하는 Matrix Factorization - non negative matrix Factorization
참고 link : https://angeloyeo.github.io/2020/10/15/NMF.html
음수를 포함하지 않는 행렬 X 를 --> 음수 포함하지 않는 행렬 W, X로 분해하는 방식
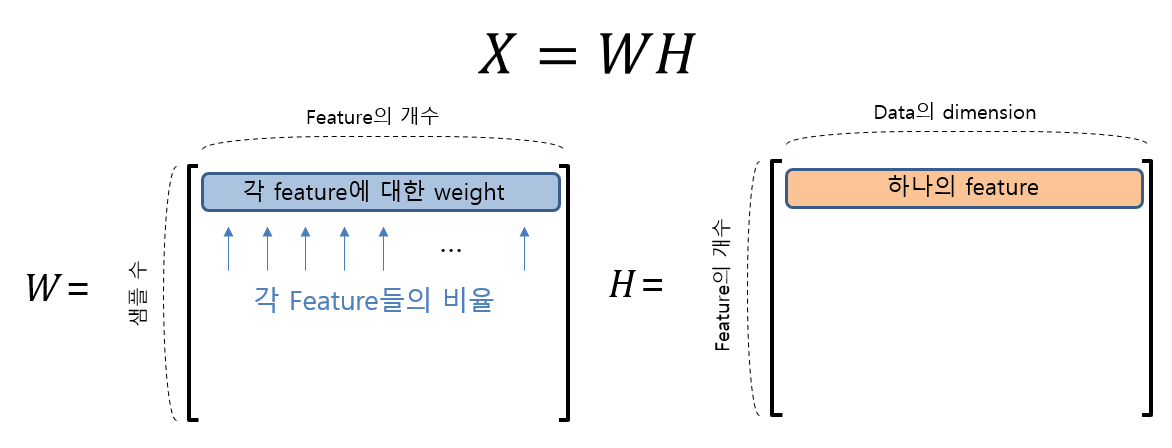
- feature의 개수는 임의로 정할 수 있음
- 각 피쳐를 얼마나 반영할건지 "각 feature 들의 비율" 을 조정
- 목표는 쪼개놓은 WH가 원래의 X와 최대한 가까웠으면 좋겠다.
(3) PMF 로 하는 Matrix Factorization
(4) Matrix Factorization의 Optimization - SGD, ALS
https://sungkee-book.tistory.com/12
[추천 시스템] Matrix Factorization (SGD)
[추천시스템 시리즈] 2021.08.30 - [데이터과학] - [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 2021.09.01 - [데이터과학] - [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MA..
sungkee-book.tistory.com
3. Factorization machine
https://greeksharifa.github.io/machine_learning/2019/12/21/FM/
Python, Machine & Deep Learning
Python, Machine Learning & Deep Learning
greeksharifa.github.io
SVM 과 factorization 모델들의 강점을 결합한 모델
1) 단순 linear regression --> 변수간의 관계가 파악이 안됨

2) Linear regression + 각 변수간의 곱으로 interaction 반영 --> 계산량이 늘어남

위 식에서 첫 째 항은 global bias, 두 번째 항은 선형 회귀, 세번 째 항이 각 feature 간의 관계를 고려한 부분이다.
각 feature별 관계를 표현할 수 있는 weight 가 필요하게 된 것이다.
3) 2번의 식을 행렬 W를 분해해보자

내부의 행 는 k개의 factor를 지닌 i번째 변수를 설명한다.
k는 0을 포함한 자연수이며, factorization의 차원을 정의하는 하이퍼 파라미터이다.
2-way FM(2차수)은 변수간의 단일 예측변수와 결과변수 간의 상호작용 뿐 아니라
pairwise한(한 쌍의) 예측변수 조합과 결과변수 사이의 상호작용도 잡아낸다.
댓글