참고 커널 코드
데이콘 대회 참여 - 03 데이터 샘플링과 종속변수 로그변환
공지 제 수업을 듣는 사람들이 계속적으로 실습할 수 있도록 강의 파일을 만들었습니다. 늘 도움이 되기를 바라며. 참고했던 교재 및 Reference는 꼭 확인하셔서 교재 구매 또는 관련 Reference를 확��
chloevan.github.io
Q1. 타겟 값의 분포를 시각화 하는 과정에서
sklearn.stats.norm.fit , sklearn.stats.probplot 구문이 등장한다. 이 메소드의 역할이 뭘까?
출처 : https://datascienceschool.net/view-notebook/e6c0d4ff9f4c403c8587c7d394bc930a/
그전에 우선 확률분포 기본 개념 링크
1) sklearn.stats.norm --> 확률 분포 객체를 생성할때 (연속형 자료 정규 분포 경우)
기댓값이 1이고 표준 편차가 2인 정규분포 객체로 만드는 것
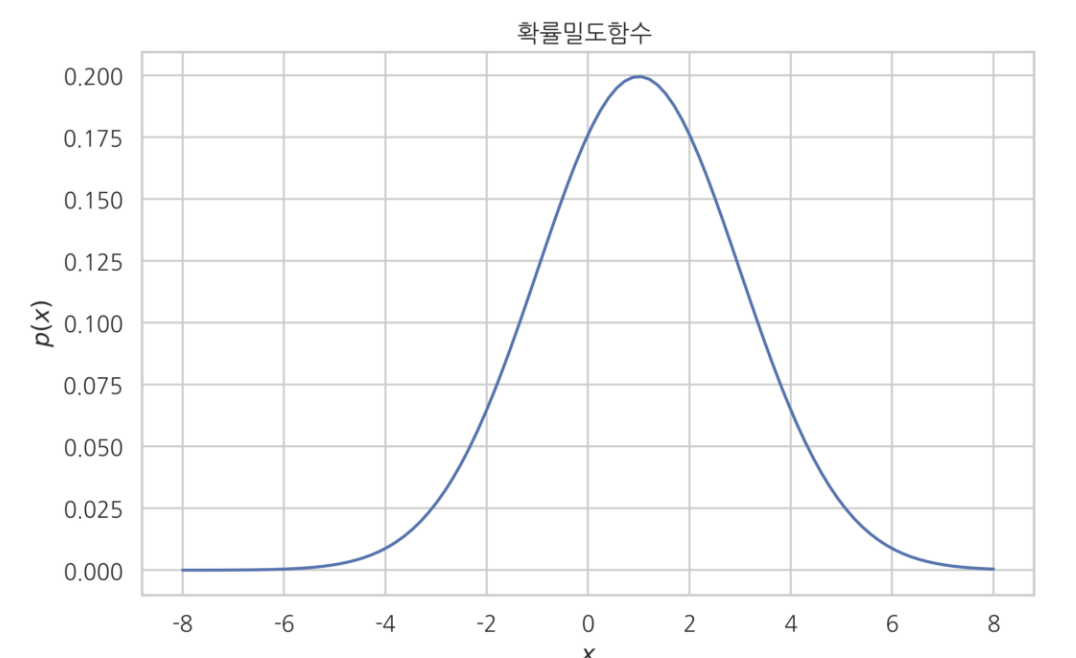
rv = sp.stats.norm(loc=1, scale=2)sklearn.stats.norm 에서 pdf 를 쓰고 안쓰고의 차이는? --> pdf는 확률 분포를 확률 밀도 함수로 반환.
xx = np.linspace(-8, 8, 100)
pdf = rv.pdf(xx)
plt.plot(xx, pdf)
plt.title("확률밀도함수 ")
plt.xlabel("$x$")
plt.ylabel("$p(x)$")
plt.show()
2) 분석하고자 하는 데이터 (df['AMT']) 의 타겟값의 확률 분포를 확인했을 때,
sns.distplot(df['AMT'] , fit=norm);
(mu, sigma) = norm.fit(df['AMT'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best')
plt.ylabel('Frequency')
plt.title('AMT distribution')
fig = plt.figure()
res = stats.probplot(df['AMT'], plot=plt)
plt.show()| sns.distplot(df['AMT'], fit = norm) 의 결과 |
stats.probplot(data['AMT'], plot=plt) 의 결과 |
 |
 |
3) stats.probplot 은 QQ plot 을 그리는 메서드
QQplot 이란? 출처 : https://datascienceschool.net/view-notebook/26f1850cd89f419993db0648bbd3c900/
Q-Q(Quantile-Quantile) 플롯은 분석하고자 하는 샘플의 분포과 정규 분포의 분포 형태를 비교하는 시각적 도구이다.
Q-Q 플롯은 동일 분위수에 해당하는 정상 분포의 값과 주어진 분포의 값을 한 쌍으로 만들어 스캐터 플롯(scatter plot)으로 그린 것이다. Q-Q 플롯을 그리는 구체적인 방법은 다음과 같다.
- 대상 샘플을 크기에 따라 정렬(sort)한다.
- 각 샘플의 분위수(quantile number)를 구한다.
- 각 샘플의 분위수와 일치하는 분위수를 가지는 정규 분포 값을 구한다.
- 대상 샘플과 정규 분포 값을 하나의 쌍으로 생각하여 2차원 공간에 하나의 점(point)으로 그린다.
- 모든 샘플에 대해 2부터 4까지의 과정을 반복하여 스캐터 플롯과 유사한 형태의 플롯을 완성한다.
- 비교를 위한 45도 직선을 그린다
| 정규 분포를 따르지 않는 경우 | 정규 분포를 따르는 경우 |
|
 |
 |

댓글