[기술면접] L1, L2 regularization, Ridge와 Lasso의 차이점 (201023)

Q. L1, L2 regularization 을 각각 설명하세요

Q. Ridge와 Lasso의 차이점

 

 

Q. L1, L2 regularization 을 각각 설명하세요 

 

 

딥러닝 모델 과적합을 막는 방법에는 세가지가 있는데 

- batch normalization. (배치정규화)

- weight regularization (정규화)

- dropout (학습당시 랜덤으로 절반의 뉴런만 사용하기)

 

이 중 두번째에 해당되는 것이 L1, L2 regularization 이다.

 

 

1. 그럼 궁금한건 L1, L2 regularization

학습을 진행할 때, 학습 데이터에 따라 특정 weight의 값이 커지게 될 수있다.

이렇게 되면 과적합이 일어날 가능성이 아주 높은데,

이를 방지하기 위해 L1, L2 regularization를 사용한다. 

각각은 앞서 언급한  l1 -norm ,  l2 - norm의 컨셉을 가져와 학습에 영향을 미치는 cost function을 조정한다. 

 

1) l1 regularization 

 

 

 

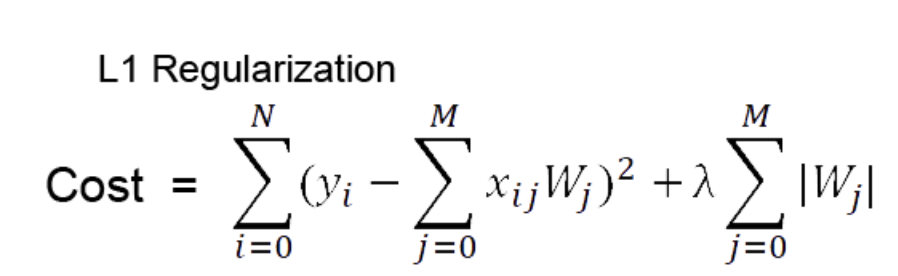
더하기 전 좌측이 일반적인  cost function이고 여기에 가중치 절대값을 더해준다. 

편미분 을 하면 w값은 상수값이 되어버리고, 그 부호에 따라 +-가 결정됨

가중치가 너무 작은 경우는 상수 값에 의해서 weight가 0이 되어버림.

 

==> 결과적으로 몇몇 중요한 가중치 들만 남게됨

 

 

2) l2 regularization

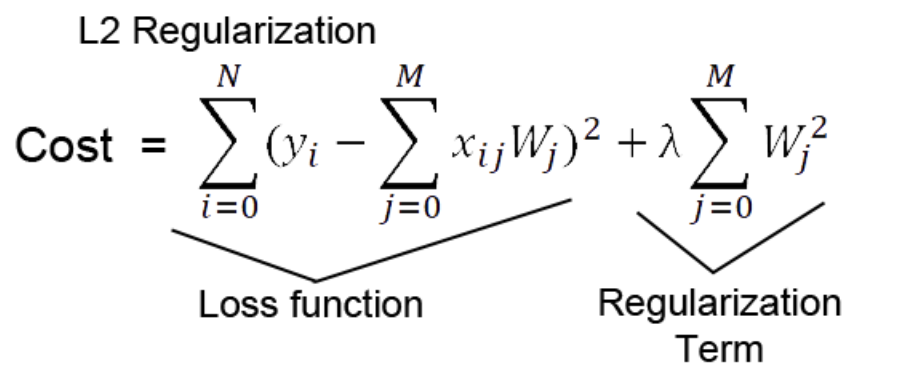
Cost function에 제곱한 가중치 값을 더해줌으로써

편미분 을 통해 back propacation 할 때

Cost 뿐만 아니라 가중치 또한 줄어드는 방식으로 학습을 한다.

특정 가중치가 비이상적으로 커지는 상황을 방지하고, Weight decay 가능해짐

즉, 전체적으로 가중치를 작아지게 하여 과적합을 방지하는 것.

 

 

 

Q. Ridge와 Lasso의 차이점

 

선형 회귀 모델에서 L1 규제 를 주는 것이 lasso regression 

선형 회귀 모델에서 L2 규제 를 주는 것이 Ridge regression 

 

 

 

+) elasticnet 은 두개다 쓰는 것

 

제약식	L2  norm	L1 norm	L1 +L2 norm
변수선택	불가능	가능	가능
solution	closed form	명시해 없음	명시해 없음
장점	변수간 상관관계가 높아도 좋은 성능	변수간 상관관계가 높으면 성능↓	변수간 상관관계를 반영한 정규화
특징	크기가 큰 변수를 우선적으로 줄임	비중요 변수를 우선적으로 줄임	상관관계가 큰 변수를 동시에 선택/배제

출처 : ratsgo.github.io/machine%20learning/2017/05/22/RLR/

Regularized Linear Regression · ratsgo's blog

 

 

 

 

 

+)) 자세히 설명  정규화 이전 우선 l1, l2 는 뭘 의미 하나 ====================================

# l1 -norm ,  l2 - norm

우리는 벡터 간의 거리를 노름(norm) 이라고하고, 여기서 거리를 구할때 두가지 방법으로 나뉘는 데 

이때 l1 -norm ,  l2 - norm 이 있다. 

 

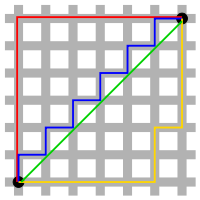
이 그림이 정말 자주 사용되지만, 공식으로 보는게 이해가 편하긴 하다. 

 

 

1) l1 -norm 

l1 -norm 은 결국 두 벡터간의 거리를 절대 값으로 구하는 거고,

\위의 그림에서 초록색을 제외한 모든 경로가 l1 -norm 이라 이해하면 됨

 

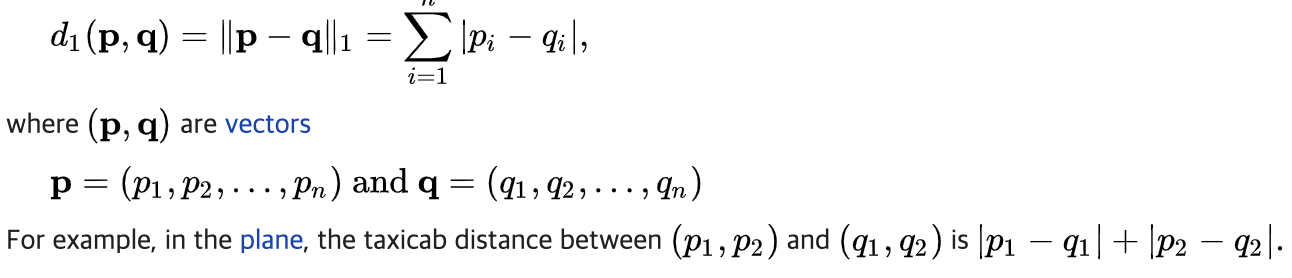
가령 A(0,0) B(1,2) 라면 사이의 l1 -norm 거리는 3 

 

 

2) l2 -norm 

 

유클리디안 거리 ! 옛날 ㅇ옛적에 배운 유클리디안 거리라고 이해하자

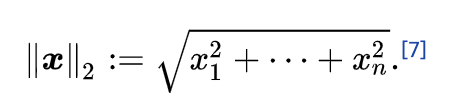
가령 A(0,0) B(1,2) 라면 사이의 l1 -norm 거리는 루트 5

 

# l1 -loss ,  l2 - loss

* l1 -loss : 타겟값과 예측값의 차를 절대 값으로 구한것

 

* l2 -loss : 타겟값과 예측값의 차의 제곱 

 

 

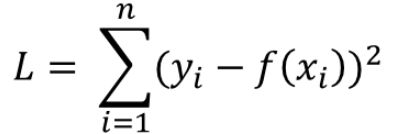
참고 링크 : 

 

junklee.tistory.com/29

L1, L2 Norm, Loss, Regularization?

light-tree.tistory.com/125

딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명