1. 문제설명
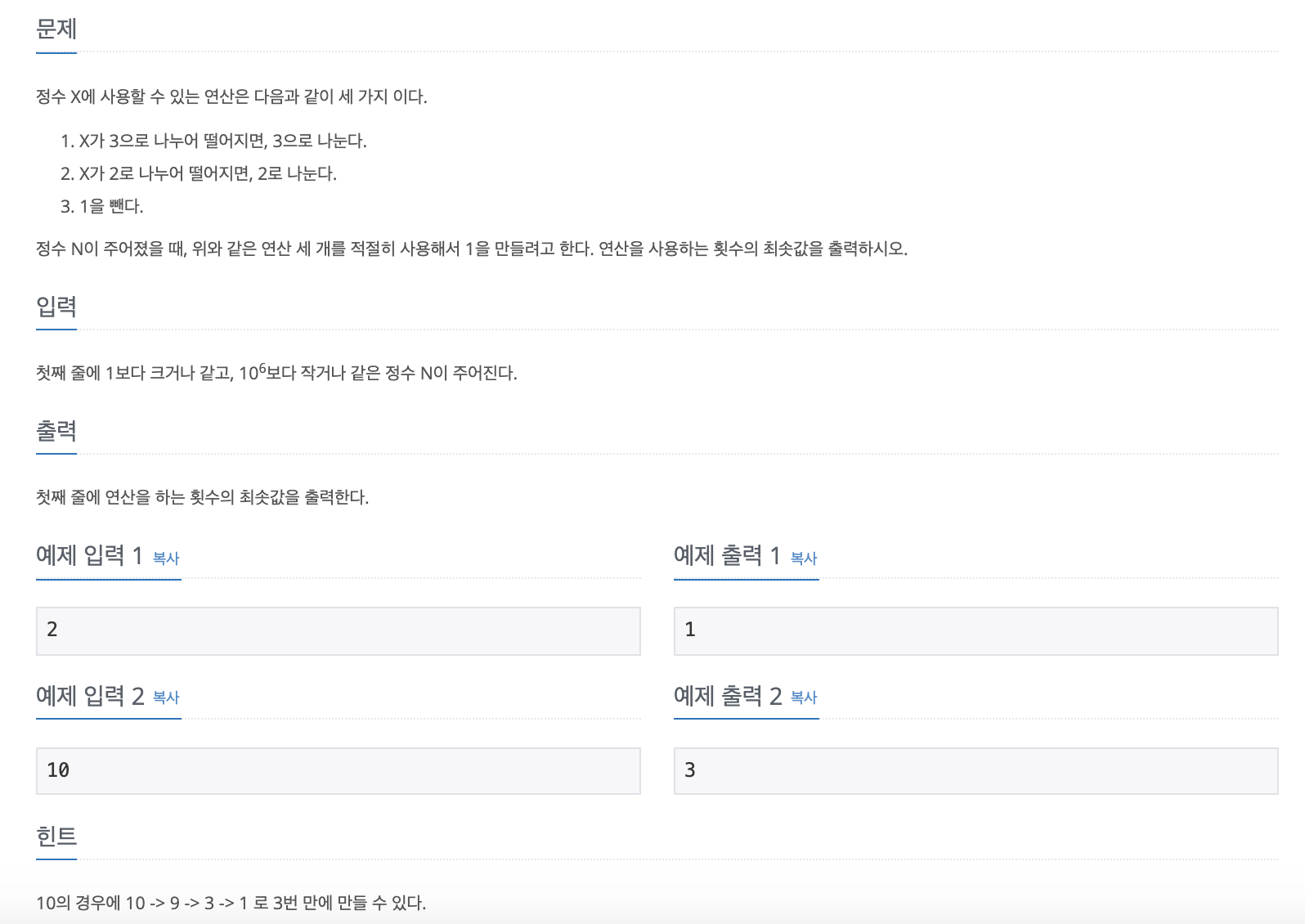
2. 풀이
어제 설탕 문제처럼 단순히 조건문으로 풀수 있다고 생각했는데 아니었다 해당문제는 전형적인 DP 문제였음
우선 조건문으로 풀었을 때,
def solution(input_num):
chk = 0
num_dict = {}
while input_num > 1:
# print(input_num)
if input_num % 2 !=0: # 홀수 경우
if input_num % 3 == 0:
input_num /= 3
else:
input_num -= 1
else: # 짝수 경우
if (input_num -1) % 3 == 0:
input_num-=1
else:
input_num /= 2
chk +=1
return chk
홀짝의 경우로 나누어서 풀었는데, 내 기준에서는 반례를 찾지 못했지만 계속 틀렸었다..
따라서 아예 DP 접근으로 시도
숫자를 하나씩 증가시켜가면서 최소 단계수 구하는데
이때 컨셉은 과거의 배수들 정보를 가져오면서 현재 수의 최소단계수를 구하는 것
- N이라는 수는 N//3을 연산전으로 돌리면, 즉 +1을 하면 만들 수 있다.
- N이라는 수는 N//2을 연산전으로 돌리면, 즉 +1을 하면 만들 수 있다.
- N이라는 수는 N-1을 연산전으로 돌리면, 즉 +1을 하면 만들 수 있다
n = int(input())
dp = [0 for _ in range(n +1)] # 최소 단계 수 담길 리스트 생성
for i in range(2, n+1): # 2 부터 n 까지 탐색
dp[i] = dp[i - 1] + 1 # 우선 이전단계에서 1 더해놓고,
# 아래의 두가지 경우에 해당되면 바꾸기
if i % 2 == 0: # 2의 배수면
dp[i] = min([dp[i], dp[int(i / 2)] + 1]) # 과거기준 1더한거 / 과거 2의배수에서 1더한거중 더작은수 비교
if i % 3 == 0:
dp[i] = min([dp[i], dp[int(i / 3)] + 1]) # 과거기준 1더한거 / 과거 3의배수에서 1더한거중 더작은수 비교
print(dp[n])
3. 정리
DP는 결국 이렇게 풀어야한다. 설탕 공장 문제도 분명 이렇게 풀수 있을테니 꼭 시도해보기
728x90
반응형
'Study > Algorithm & Data structure' 카테고리의 다른 글
| [백준][DP] 9095번 1,2,3 더하기 python (200923) (0) | 2020.09.23 |
|---|---|
| [백준][DP] 11053번 가장 긴 증가하는 부분 수열 python (200922) (0) | 2020.09.22 |
| [백준][DP] 2839번 설탕 배달 python (200920) (0) | 2020.09.20 |
| [프로그래머스][DP] N으로표현 python (200920) (0) | 2020.09.20 |
| [백준][DP] 2193번 이친수 python (200919) (0) | 2020.09.19 |



댓글