0. DP
DP의 핵심 컨셉은 그때 그때 결과값을 저장해두고 그걸 불러오는 방식이다.
www.fun-coding.org/Chapter14-dp_divide.html
파이썬과 컴퓨터 사이언스(기본 알고리즘): 동적 계획법과 분할 정복 - 잔재미코딩
프로그래밍 연습 피보나치 수열: n 을 입력받아서 다음과 같이 계산됨 n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요 함수를 fibonacci 라고 하면, fibonacci(0):0 fibonacci(1):1 fibonacci(2):1 fibon
www.fun-coding.org
여기서도 그걸 적용해보자 !
1. 문제 설명

2. 풀이
def solution(triangle):
height = len(triangle)
up_tri = triangle.copy()
root = triangle[0][0]
for l_idx in range(1,height): # 처음 루트는 제외
for n_idx in range(len(up_tri[l_idx])):
if n_idx == 0: # 맨 첫 노드이면 바로 윗단계 맨 첫노드만 더해
up_tri[l_idx][n_idx] += up_tri[l_idx - 1][0]
elif n_idx == len(up_tri[l_idx])-1: # 맨끝노드면 바로 윗단계 맨 끝노드만 더해
up_tri[l_idx][n_idx] += up_tri[l_idx - 1][-1]
else: # 둘다 아닌 중심노드들이면 바로 위 좌우 노드들 중 큰수(up_max_val)를 더해준다.
up_max_val = max(up_tri[l_idx - 1][n_idx-1],up_tri[l_idx - 1][n_idx])
up_tri[l_idx][n_idx] += up_max_val
print(up_tri)
return max(up_tri[-1])
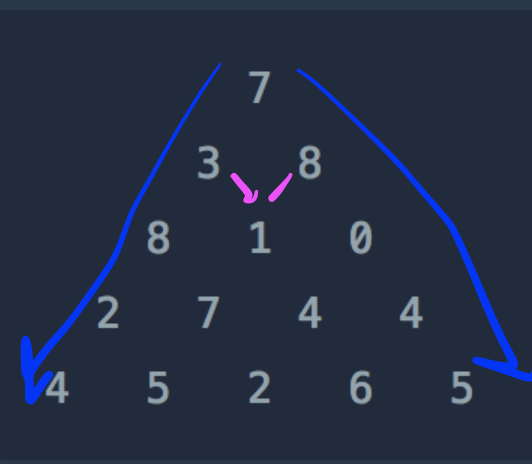
여기서는 두가지 경우로 나눠야한다.
파란색 처럼 코너에 있어서 위레벨의 첫 or 끝 숫자를 받아서 더해주는 경우
핑크색 처럼 중심에 있어서 위레벨의 좌우 숫자중 큰거를 받아서 더해주는 경우
각 레벨별로 업데이트 결과를 찍어보면 다음과 같다
[[7], [10, 15], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
[[7], [10, 15], [18, 16, 15], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
[[7], [10, 15], [18, 16, 15], [20, 25, 20, 19], [4, 5, 2, 6, 5]]
[[7], [10, 15], [18, 16, 15], [20, 25, 20, 19], [24, 30, 27, 26, 24]]
그리고 이 마지막 단계에서 가장 합을 뽑아주면 되는 아주 간단한 문제.
결국 누적합이 핵심이다 ! ****
3. 정리
결국, 각 레벨의 합들을 저장해주면서, 이 저장된 값을 불러와 다시 다음단계를 쌓아가는 방식
풀이를 보고나니 DP의 가장 기본적인 접근 문제 였던거 같다.
DFS 경로 문제로 풀려 했었다. 하나하나씩 들어가보면서... 최대값 구하는 방식으로... (생각만해도 머리아픔)
하지만, 경로를 묻지 않고 최대값만 묻는 문제였으니 그렇게 풀면 안되고, 바로 윗단계의 합만 가져와서 풀면됨
아직 이러한 문제를 마주했을때, DFS인지 BFS인지 DP 인지 구분이 잘 안된다.
문제를 더 풀면 감이 오겠지
'Study > Algorithm & Data structure' 카테고리의 다른 글
| [프로그래머스][DP] N으로표현 python (200920) (0) | 2020.09.20 |
|---|---|
| [백준][DP] 2193번 이친수 python (200919) (0) | 2020.09.19 |
| [프로그래머스][stack] 사전순 부분문자열 (200903) (0) | 2020.09.03 |
| 코테 유형별 풀이법 (내나름 정리) (0) | 2020.08.28 |
| [백준][Greedy] 1931번 문제 - 회의실배정 python (200804) (0) | 2020.08.04 |

댓글