[Deep Learning] VAE (Variational Auto Encoder) 개념 정리
https://www.youtube.com/watch?v=GbCAwVVKaHY&t=546s
위 강의 링크 내용을 정리해서 요약한 내용입니다.
추가 참고 link :
https://hugrypiggykim.com/2018/09/07/variational-autoencoder%EC%99%80-elboevidence-lower-bound/
https://di-bigdata-study.tistory.com/4
VAE (Variational Auto Encoder)
0. ae와 vae 의 차이점?


- ae 의 핵심은 원래의 데이터를 복원 (x --> x), 핵심은 Z를 잘 임베딩 하는 것 (manifold learning)
+) 원래의 DB를 고차원의 공간에 잘 표현하는 것이 manifold learning 의 목적
- 반면 vae는 원래의 데이터를 새로운 유사한 데이터로 재생성(x --> x')해 내는 것 (generative model)
--> 둘은 목적 자체가 완전히 다른 모델 !!!!
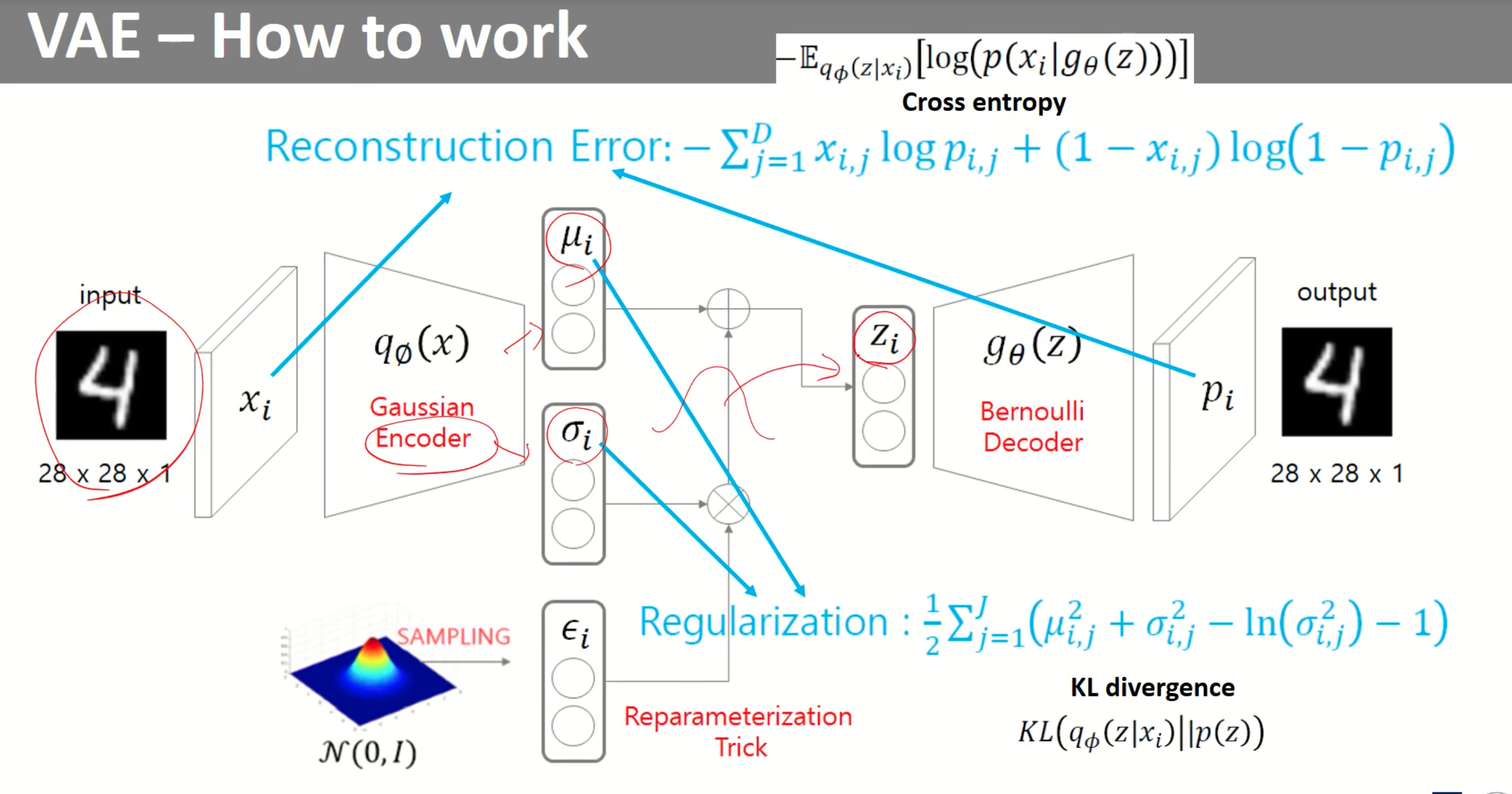
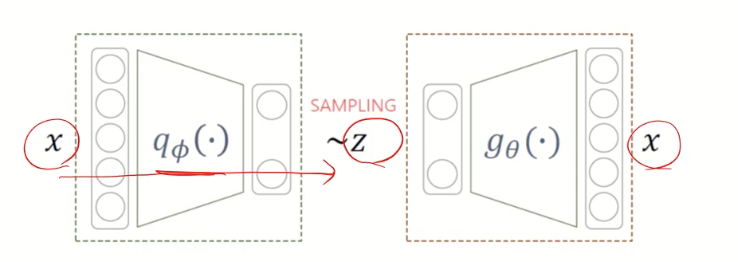
1. vae 구조 뜯어보기

(AE는 encoder --> z --> decoder)
1) encoder (gaussian)
- input - Xi
- output - gausian encoder를 거친후 두 개의 벡터를 반환
기존의 AE모델은 n차원의 벡터를 반환했다면
VAE에서는 n차원의 평균(μ), n차원의 표준편차(σ) 값을 반환 → n개의 분포가 생김 → n개의 정규 분포에서 Z를 샘플링
2) Z를 샘플링 - Reparametererization Trick
- 샘플링을 하는 것은 미분가능한 수식을 나타낼 수 없음 (backpropagation 안됨) → Reparametererization Trick 적용 !!
- Reparametererization Trick : 표준 정규분포에서 샘플링을 한 값 표준편차 σ에 곱한 뒤 μ 더함 → μ + ( ϵ * σ )
→Z를 표준 정규 분포로 만드는 과정이라 이해 !
3) decoder (bernoulli)
- input - $Z_{i}$ (표준 정규분포)
- output - Pi
2. loss function
+) loss function
확률을 normal (=gaussian) distribution 정규 분포라 가정하면 ==> 회귀니까 손실함수는 MSE
확률을 bernoulli distribution, 이산확률 분포라 가정 ==> 분류니까 손실함수는 Cross entropy
---> decoder를 통과해서 나온 $p_{i}$가 베르누이 분포를 띄고있기 때문에 Cross entropy 적용
+) 가능도 Likelihood
L(distribution|data) = likelihood
여기선 입력 데이터는 고정되어있지만 분포는 변하는 상황, 데이터가 주어졌을때 분포가 데이터를 얼마나 잘 설명하는가
+) Maximum Likelihood
각각의 관측값에 대해서 총 가능도가 (모든 가능도의 곱) 최대가 되게 하는 분포를 찾는 것
최대가능도 추정법(Maximum Likelihood Estimation, MLE)은 주어진 표본에 대해 가능도를 가장 크게 하는 모수
𝜃 를 찾는 방법이다.
Loss 는 크게 원본의 이미지를 구현하기 위한 목적 함수 Reconstruction error와
Encoder output인 평균과 표준편차를 정규화 하는 Regularization error 가 있다.
1) Reconstruction Error - AE 의 loss function
- VAE에서 decoder의 output $p_{i}$ 는 베르누이 분포(이진분류) 를 따른다고 가정
- predicted value $p_{i}$ 와 target value $x_{i}$ 의 차이를 구하기 위해 cross entropy 계산
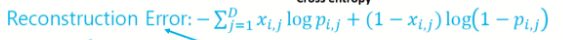

2) Z가 normal distribution을 따라야 한다는 Regularization error - KL divergence
표준 정규분포에서 샘플링 된 값 p(z)과
encoder output 인 $q_{\phi}(z|x_{i})$ 의 차이가 적도록 KLdivergence 계산

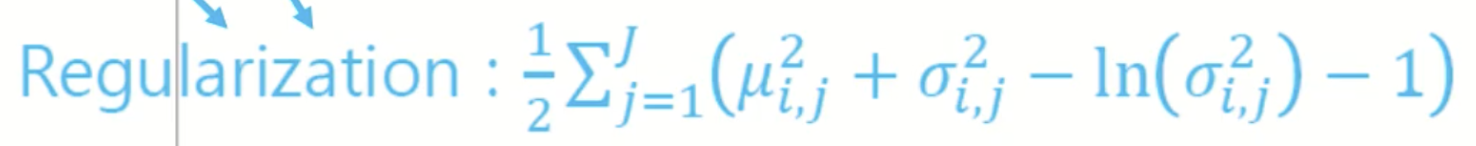
3. loss function 뜯어보기
1) decoder output이 X일 확률 - $p_{\theta}(x)$ 를 구해보자
- decoder input은 $p_{\theta}(z)$ output은 $p_{\theta}(x|z^{(i)})$
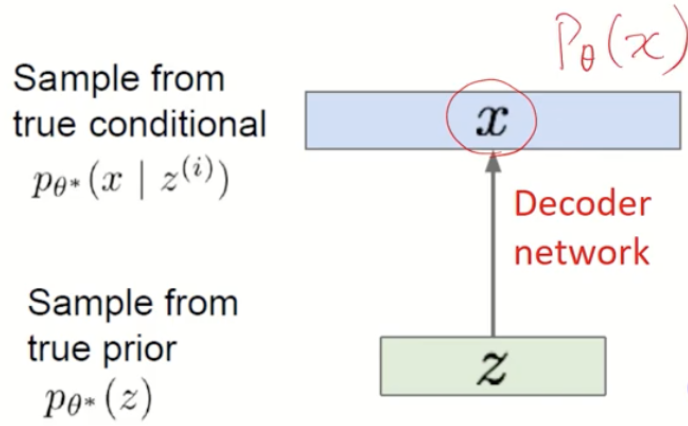
- 우리는 training data의 likelihood를 최대화하는 확률 분포를 갖는게 목표
즉, decoder output이 X일 확률 $p_{\theta}(x)$ 를 최대화하는 확률 분포를 갖는게 목표
2) $p_{\theta}(x)$ 를 최대화 해보자 !
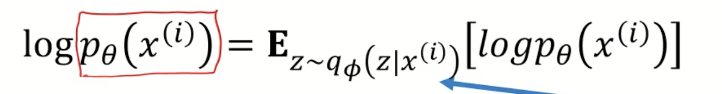
- 아까 우리는 $p_{\theta}(x^{(i)}$의 값을 최대화 하는 것이 목표였음
- 우선 $p_{\theta}(x)$ 앞에 로그를 씌움
여기서 $p_{\theta}(x)$ 는 encoder를 거친 z를 입력 받은 뒤 다시 decoder를 거쳐 나온 값이므로
z가 encoder의 확률 distribution을 따름--> $z~q_{\phi}(z|x^{i})$
- 이후 식을 베이즈 정리를 적용하고 아래와 같이 쭉쭉 전개하면

- 이렇게 전개된 맨 마지막 식을 아래의 수식을 참고해서 바꾸면.. 2번째항 3번째 항은 KL divergence 식으로 바꿀 수 있음
(KL divergence : 두 확률분포의 차이를 계산하는 데에 사용하는 함수)

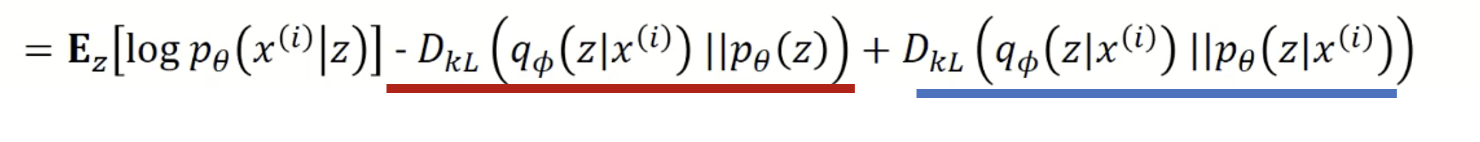
(p는 true 확률, q는 추정 확률)
첫번째 : Z에서 X가 나올 확률 (decoder 의 true 값)
두번째 : encoder의 output $q_{\phi}(z|x)$ 과 Z와 distribution $p_{\theta}(z)$ 의 차이
세번째 : encoder의 output $q_{\phi}(z|x)$ 과 $p_{\theta}(z|x)$의 차이
하지만 세번째 항에서 p(z|x)는 계산 할 수 없음
(다만 KLD 차이기 때문에 0보다 크거나 작다는 것만 알 수 있음)

세번째 항이 항상 0보다 크거나 같으므로 위 사진 처럼 부등식으로 표현이 가능하다. 이를 ELBO라 부른다.
+) Q 그럼 p(x|z)랑 p(z)는 어떻게 구하는 건지...
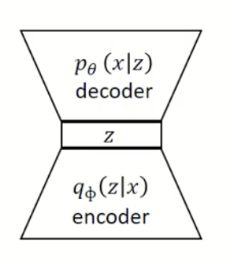
p(z)는 vae에서 표준 정규분포라고 가정을 한다.
p(x|z)는 z라는 표준 정규 분포가 주어졌을 때 , xi를 가질 확률 --> decoder
그러나 p(z|x)는 구할 수 없음 - 역방향
3) ELBO (evidence lower bound)
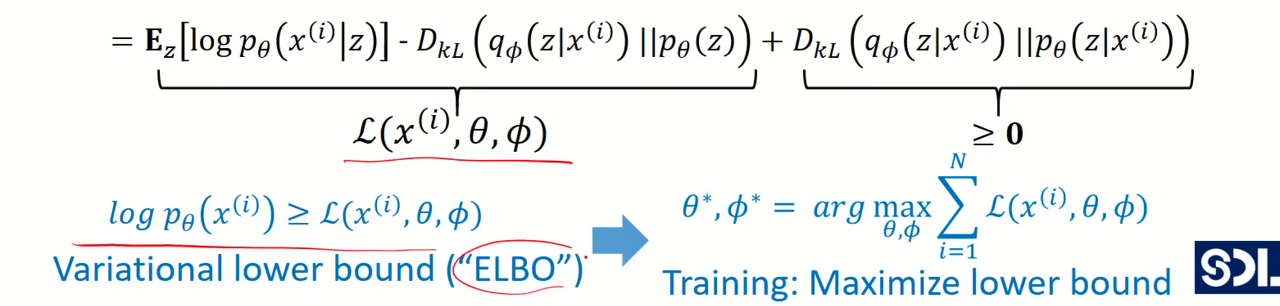
- ELBO를 maximize함으로써 likelihood 또한 maximze할 수 있는 것임
- ELBO를 maximize 하는 학습 파라미터 decoder 파라미터 $\phi$, encoder 파라미터 $\theta$ 구하기
4) 최종적으로 Maximize 을 minimize로 바꾸면

--> Reconstruction error :
x가 주어졌을 때 $q_{\phi}$ 인코더 네트워크를 지나서 z 생성 --> $q_{\phi}(z|x)$
그 z가 $q_{\theta}$ 디코더 네트워크를 지났을 때 --> $q_{\theta}(z)$
xi가 등장할 확률
--> Regularization :
x가 주어졌을 때 $q_{\phi}$ 인코더 네트워크를 지나서 z 생성 --> $q_{\phi}(z|x)$
우리가 가정한 분포 (표준정규분포) p(z)와 유사하도록 만드는 것
3. Optimization (이제 계산을 해보자)
1) reconstruction error
가정 1. $p_{\theta}$는 베르누이를 따른다고 가정 --> cross entropy로 계산
decoder의 아웃풋이 x가 등장할 확률 (classification)

- 모든 z에 대해서 적분한다는 것은 불가능 ! 따라서 몬테 카를로 테크닉을 활용
# 몬테카를로 테크닉
몬테카를로 : "샘플링" 이라고 이해하면 됨
어떤 분포를 가정하고 그 분포에서 굉장히 여러번 샘플링을 해서 평균을 내면
전체에 대한 기댓값과 샘플링한 것들의 기댓값은 같아질꺼다~ 하는 컨셉
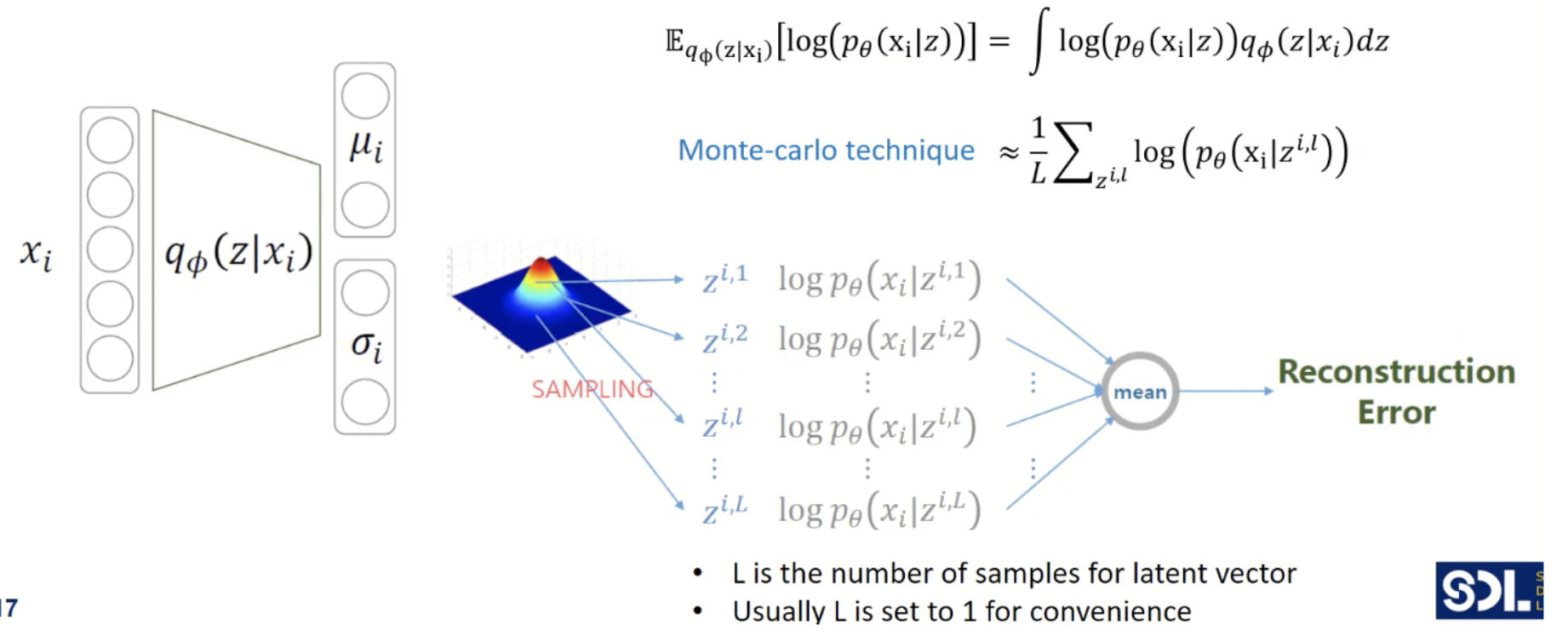
- 따라서 몬테카를로 기법 적용 (무수히 여러번 샘플링을 해서 모집단의 평균 찾기) --> 하지만 계산량이 너무 많아짐
- 결국 샘플링을 한번만 한 뒤 이걸 대표값이라 하고 위의 식 계산 (L을 1로 가정함)
+) 하지만 샘플링 과정은 미분이 안됨 --> Backpropagation 불가능 --> 그래서 적용한게 reparameterization trick
( 자세한 설명은 맨뒤에..)

==> 최종적으로 $log(p_{\theta}(x_{i}|z^{i}))$
이제 $p_{\theta}$ 가 어떤 확률 분포를 따르는지 가정하느냐에 따라서
reconstruction error 수식이 바뀜
가정 a. $p_{\theta}$는 베르누이 분포를 따른다고 가정 --> Cross entropy 계산
- decoder의 output : x가 등장할 확률 Pi

- 일단은 z가 들어가서 pi로 복원이 되면, 차원이 5라고 한다면 각각 5개에 대한 확률을 계산
확률 곱으로 표현해서 --> 합으로 바꾼뒤
- (2번째줄) 따라서 $p_{\theta}(x_{i}|z^{i})$ 를 베르누이 식으로 바꿈 (2번째줄)
- (3번째줄) 위의 식은 cross entropy 식으로 바꿔서 계산
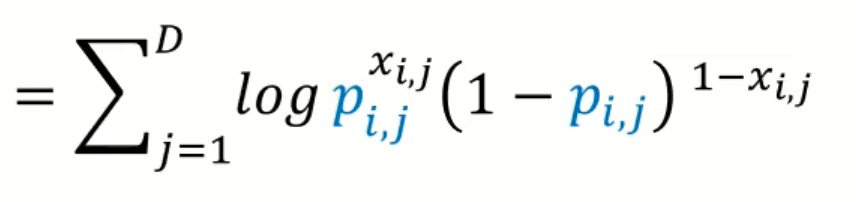
가정 b. $p_{\theta}$는 가우시안 분포 (정규분포) 를 따른다고 가정 --> squared Error 계산
decoder의 아웃풋이 x의 평균과 표준편차

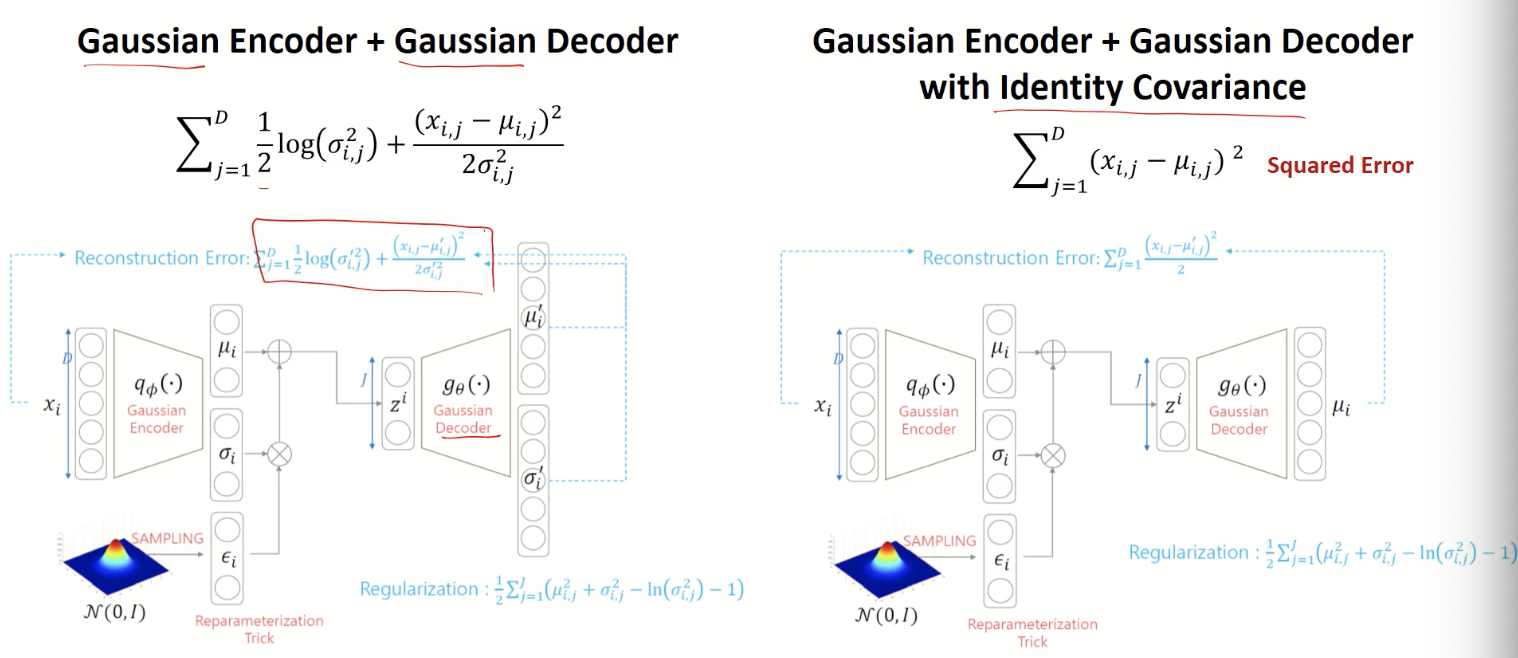
2) regularization

- 가정 1. encoder output인 $q_{\phi}(z|x)$ 는 정규분포를 띈다
- 가정 2. p(z)는 표준 정규분포를 띈다.
- 이 두 분포를 같게 만들어준다 --> KL divergence를 통해서

+) reparameterization trick
** 샘플링하는 과정에서 Reparametererization Trick 을 사용 : 이게 샘플링을 최적화 하는 방법 중에 하나 (미분 가능하게 바꿔줌)

- 미분가능한 식으로 만들기 위해 표준정규분포에서 샘플링을 한 뒤 (epsilon)
- encoder output의 std에 곱해주고 거기에 mean 값을 더해 Z를 만듦
- 따라서 좌측에서는 Z가 정규 분포로 부터 샘플링을 한다는 정보만 있을 뿐 미분을 위한 식을 도출 할 수 없었는데,
우측에서는 표준 정규분포의 epsilon을 활용해 식을 만들어냄
+) 이게 무슨 의미가 있나?
샘플링된 표준 정규 분포를 encoder output과 연결시켜 같이 학습 될 수 있도록 함
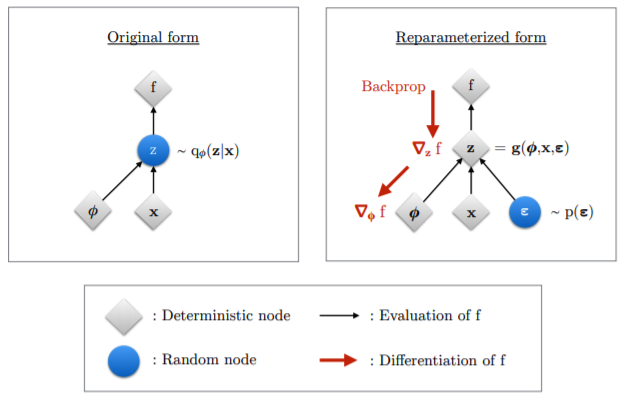
5. 결론
- 생성모델에 대한 수학적인 접근이 이뤄짐
- Decoder 를 통해 생성된 학습 데이터는 기존의 input 데이터와 닮아있다. (아주 다른 형태의 데이터가 나오긴 어려움)
- 그러나 생성의 품질이 GAN 모델만큼 좋지는 못함
+) next step - 추천 알고리즘에서의 vae 활용
1. multi vae (Variational Autoencoders for Collaborative Filtering)
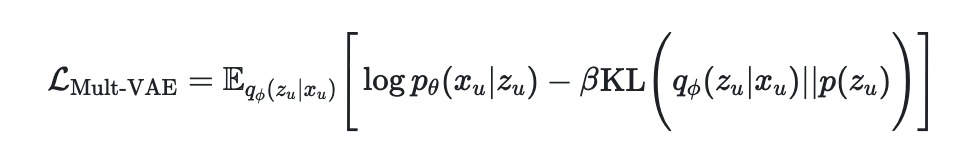
" likelihood p_{\theta}(x_{u}|z_{u})가 다항분포를 따른다"
Mult-VAE는 VAE 와 다르게 가우시안 베르누이 분포가 아닌 다항분포를 likelihood function에 적용
Generative model은 유저 u에대한 k차원의 latent 로 샘플링하여 $f_{\theta}: \R^{k} \rightarrow \R^{|I|}$ 로 차원 변경을 해주고 상호작용 $n_{u}$ 를 multinomial distribution에서 도출
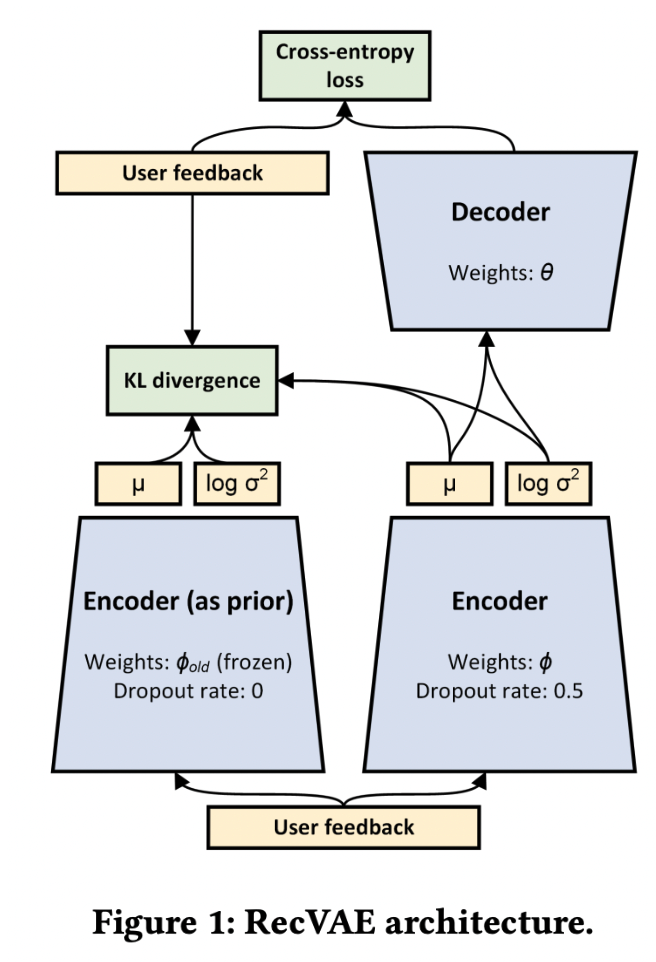
2. RecVAE